- ...;2.1
- in
generale, per la (1.15), in tutte le trasformazioni lineari
il vettore delle coordinate trasforma sempre con la matrice associata alla
trasformazione, dato che quest'ultima è anche lo jacobiano.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... invece2.2
- in realtà abbiamo visto in
§1.1.2 che è uno pseudoscalare.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....2.3
- o
meglio è uno pseudoscalare, così come lo è
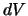 nello spazio euclideo.
nello spazio euclideo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Eulero-Lagrange:2.4
- per una trattazione completa ad esempio vedi
[LDL]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... potenziale3.1
- piccoli vuol
dire trascurabili rispetto alla massa
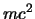 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
originale.3.2
- si noti come la posizione di
 sia
necessariamente sulla destra rispetto all'operatore.
sia
necessariamente sulla destra rispetto all'operatore.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
definito4.1
- la funzione
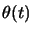 è quella definita in
(2.109).
è quella definita in
(2.109).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... discreto;4.2
- questo permette di
semplificare la notazione usando una base numerabile, nel caso generale si
dovrebbe sommare sulle soluzioni discrete ed integrare per la parte
continua, ma il risultato alla fine, sia pure con delle maggiori
complicazioni dal punto di vista dei conti, sarebbe lo stesso.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... noto,4.3
- basta costruirlo
usando la (3.8).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ottiene4.4
- basta integrare su
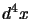 e cancellare le delta che vengono
fuori con l'altra integrazione su
e cancellare le delta che vengono
fuori con l'altra integrazione su 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... forma4.5
- ovviamente si deve
sostituire alla sommatoria, usata per le soluzioni discrete, un integrale,
avendo a che fare con soluzioni continue.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.