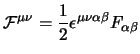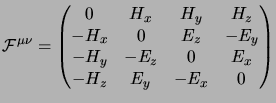La formulazione relativistica

Vediamo ora come formulare l'elettromagnetismo col formalismo relativistico; abbiamo detto che il secondo postulato (cioè la costanza della velocità della luce) è equivalente a dire che le equazioni di Maxwell devono essere valide in tutti i sistemi inerziali: questo è il primo dato da cui partire per esprimerle col formalismo dello spazio di Minkowsky.

L'altro dato è la conservazione della carica, legge anch'essa valida in tutti i sistemi di riferimento; ma la fisica ci dice di più, gli esperimenti mostrano infatti che la carica è quantizzata in multipli interi della carica elementare del protone, e che non si osserva nessuna variazione della medesima con la velocità; questo significa non solo che la carica si conserva (così come l'energia), ma anche che essa è invariante, resta cioè uguale in tutti i sistemi inerziali.

Se partiamo da quest'ultima considerazione otteniamo allora che la densità di carica che compare nelle equazioni di Maxwell non può essere invariante, essa infatti è definita dalla relazione $dq=\rho dV$ e l'elemento di volume $dV$ non è invariante; lo è invece^2.2 $d^4x$, che possiamo scrivere come:

$$d^4x = c dt dV = c d\tau \gamma dV$$

e siccome $c$ e $d\tau$ sono invarianti lo è anche $\gamma dV$.^2.3

Allora usando questa relazione dalla definizione della densità di carica data sopra otteniamo che, essendo $dq$ invariante, è invariante anche $\rho/\gamma$, e per vedere quanto vale basta andare nel sistema solidale: lì $\gamma=1$ e $\rho=\rho_0$, quindi in generale si otterrà che:

$$\rho=\rho_0\gamma={\rho_0\over{\sqrt{1-{\beta^2}}}}$$ (2.70)

e dato che $\rho_0$ è evidentemente un invariante, potremo definire il quadrivettore:

$$j^\mu = \rho_0v^\mu = \rho_0(\gamma c, \gamma{\bf v}) = (\rho c, \rho{\bf v}) = (\rho c, {\bf J})$$ (2.71)

e si ottiene l'importantissimo risultato che sebbene né $\rho$ né $\mathbf{J}$ siano invarianti, insieme formano le componenti di un quadrivettore, cosicché diventa facilissimo vedere le proprietà di trasformazione delle quantità che descrivono le sorgenti del campo da un sistema inerziale ad un altro.

Visto che abbiamo espresso le sorgenti tramite $j^\mu$ è naturale cercare di formulare le equazioni di Maxwell in forma covariante, per questo ci occorrono le derivate che abbiamo visto al §1.1.2. Allora potremo vedere come alcune delle relazioni dell'elettromagnetismo espresse al paragrafo precedente trovino una immediata ed elegante espressione in forma relativistica.

Partiamo dall'equazione di continuità: sappiamo che $j^\mu$ è un vettore controvariante, per cui possiamo scriverci immediatamente:

$$\partial_\mu j^\mu={1\over c}{\partial{j_0}\over \partial t}+\pd{},{x_i}{j_i}={\partial{\rho}\over \partial t}+\nabla\cdot{\bf J}$$

per cui l'equazione di continuità si ottiene immediatamente come:

$$\partial_\mu j^\mu=0$$ (2.72)

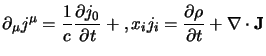
Adesso passiamo alle equazioni per i potenziali, se definiamo il quadripotenziale $\phi^\mu=(\varphi, {\bf A})$ si vede subito che si possono compendiare tutte le (1.69) per i potenziali con l'espressione:

$$\square \phi^\mu={4\pi\over c}j^\mu$$ (2.73)

il che sostanzialmente ci dice (dato che le equazioni si sanno valide, che il dalambertiano è uno scalare e che $j^\mu$ è un vettore) che anche $\phi^\mu$ è un vettore controvariante. Infine è immediato esprimere la gauge di Lorentz come:

$$\partial_\mu \phi^\mu=0$$ (2.74)

mentre una trasformazione di gauge può essere espressa come:

$$\phi^\mu\to\phi^{\prime\mu}=\phi^\mu+\partial^\mu \psi$$ (2.75)

Più complesso invece è esprimere le equazioni dei campi; infatti per i potenziali si hanno quattro funzioni incognite che è naturale associare immediatamente alle componenti di un quadrivettore; ma le componenti dei campi sono sei, ed in un quadrivettore non ci stanno.

A noi però farebbe estremamente comodo poter associare queste componenti ad una qualche quantità dello spazio di Minkowsky perché in tal modo ne otterremmo immediatamente le proprietà di trasformazione; si può notare allora che un tensore del secondo ordine antisimmetrico, in uno spazio a quattro dimensioni, ha effettivamente sei componenti indipendenti; il tentativo dunque sarà quello di esprimere i campi, partendo dai potenziali, attraverso un tensore di questo tipo.

Noi conosciamo le espressioni (1.66) che danno i campi noti i potenziali; il modo più semplice di costruire un tensore antisimmetrico a partire da essi è definire:

$$F_{\mu\nu}=\partial_\mu \phi_\nu-\partial_\nu\phi_\mu$$ (2.76)

la prima cosa da verificare è che esso sia invariante per trasformazioni di gauge; usando questa definizione e la (1.75) è immediato verificarlo, grazie alla proprietà di commutazione delle derivate, infatti:

$$F'_{\mu\nu} = \partial_\mu (\phi_\nu+\partial_\nu \psi)-\partial... ...psi-\partial_\nu\partial_\mu \psi = \partial_\mu \phi_\nu-\partial_\nu\phi_\mu$$

per cui alla fine $F'_{\mu\nu}=F_{\mu\nu}$.

Adesso si tratta di vedere cosa sono le sue componenti; evidentemente $F_{\mu\mu}=0$ e $F_{\mu\nu}=-F_{\nu\mu}$ per cui basterà considerare solo le componenti con $\mu<\nu$. Cominciamo allora con:

$$F_{0,i}=\partial_0 \phi_i-\partial_i \phi_0= -\ic{\partial{}\over... ...\varphi=\left[-\nabla_i\varphi -\ic{\partial{A_i}\over \partial t}\right] =E_i$$

(ricordiamo che avendo preso il vettore dei potenziali in forma controvariante si ha che $\phi_i=-A_i$) mentre se prendiamo $F_{ij}$ otteniamo:

$$F_{ij}=\pd{A_i},{x_j}-\pd{A_j},{x_i}$$

che si riconoscono subito come le componenti di ${\bf H}=\nabla\times{\bf A}$, e più precisamente:

$$\begin{aligned} F_{12} &= \displaystyle\pd{\phi_1},{x_2}-\p... ...\phi_3},{x_2} = \pd{A_y},{z}-\pd{A_z},{y} =-H_x \end{aligned}$$

per cui il tensore $F_{\mu\nu}$, detto anche tensore elettromagnetico, assume la forma:

$$F_{\mu\nu}= \begin{pmatrix}0 & E_x& E_y& E_z\cr -E_x & 0&-H_z& H_... ...y & H_z& 0&-H_x\cr -E_z &-H_y& H_x& 0\cr \end{pmatrix}<tex2html_comment_mark>26$$ (2.77)

questa è l'espressione per il tensore covariante, si può passare anche all'espressione controvariante usando la relazione $F^{\mu\nu}=g^{\mu\alpha}g^{\nu\beta} F_{\alpha\beta}$ che comporta poi che:

$$F^{\mu\nu}=\partial^\mu \phi^\nu-\partial^\nu\phi^\mu$$

e facendo i conti si ottiene che la sola differenza fra i due è il cambiamento di segno delle componenti date dal campo elettrico.

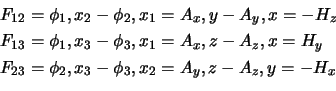
Adesso vogliamo esprimere le equazioni di Maxwell; avendo un tensore del secondo ordine la cosa più semplice da fare per derivarlo è contrarre con $\partial^\mu$; allora possiamo provare a considerare cosa viene dall'equazione:

$$\partial^\mu F_{\mu\nu}={4\pi\over c}j_\nu$$ (2.78)

queste sono quattro equazioni, e basta svolgere i conti per verificare che esse corrispondono alle due equazioni di Maxwell che coinvolgono le sorgenti. Talvolta questa equazione viene scritta anche come:

$$\div F_{\mu\nu}={4\pi\over c}j_\nu$$

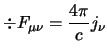
Restano da scrivere le due equazioni omogenee per i campi, che sono altre quattro componenti; viene allora naturale provare ed esprimerle tramite il rotore (che abbiamo definito al §1.1.2) come:

$$\rot F_{\mu\nu} = \half \epsilon^{\alpha\beta\mu\nu} \partial_\beta F_{\mu\nu} = 0$$ (2.79)

che, ricordando l'espressione del rotore che avevamo trovato, si potrà scrivere come:

$$\partial_\lambda F_{\mu\nu}+\partial_\nu F_{\mu\lambda}+ \partial_\nu F_{\lambda\mu}=0$$ (2.80)

(per tutte le quattro combinazioni per cui $\lambda\ne\mu\ne\nu$). In questa forma può essere facilmente verificato, facendo i conti con le componenti, che le quattro equazioni ottenute corrispondono effettivamente alle due equazioni di Maxwell (1.64b) e (1.64c). Inoltre, dato che il tensore elettromagnetico è antisimmetrico, è ancor più facile verificare la relazione è vera anche se due qualunque degli indici sono uguali, per cui alla fine la (1.80) è un'equazione che vale in generale.

Un altro modo per riscrivere queste equazioni è quello di introdurre, tramite il tensore di Ricci, il tensore di campo duale:

$${\cal F}^{\mu\nu}={1\over 2} \epsilon^{\mu\nu\alpha\beta}F_{\alpha\beta}$$

che calcolato esplicitamente diventa:

$${\cal F}^{\mu\nu}= \begin{pmatrix} 0& H_x& H_y& H_z\cr -H_x& 0& E_z&-E_y\cr -H_y&-E_z& 0& E_x\cr -H_z& E_y&-E_x& 0\cr \end{pmatrix}$$

e con questo si può riscrivere la (1.79) come:

$$\partial_\mu {\cal F}^{\mu\nu}=0$$

e, come si può verificare immediatamente svolgendo i conti per componenti, si riottengono subito le equazioni di Maxwell omogenee.