



Next: Formulazione lagrangiana del moto
Up: Formulazione lagrangiana
Previous: Formulazione lagrangiana
Contents
Index
Formulazione lagrangiana del moto di una particella libera
La formulazione lagrangiana della meccanica relativistica si costruisce per
analogia con la meccanica classica; il punto di partenza è sempre il principio
di minima azione; in meccanica classica l'azione è definita a partire dalla
lagrangiana del sistema 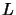 , che in generale è funzione solo delle
coordinate
, che in generale è funzione solo delle
coordinate 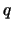 e delle loro derivate
e delle loro derivate 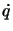 (il moto è completamente
determinato dalla posizione e dalla velocità iniziale) come:
(il moto è completamente
determinato dalla posizione e dalla velocità iniziale) come:
 |
(2.96) |
e dal principio di minima azione si ottengono le equazioni di
Eulero-Lagrange:2.4
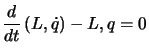 |
(2.97) |
che sono le equazioni del moto.
La lagrangiana di una particella libera poi si può ottenere con considerazioni
del tutto generali (vedi sempre [LDL]) dall'isotropia dello spazio e
del tempo e dal principio di relatività galileiana, come:
Come si vede tutte queste espressioni non sono Lorentz-invarianti, e si tratta
dunque di trovarne delle opportune estensioni. Prendiamo allora come punto di
partenza il principio di minima azione, se questo deve continuare a valere si
ha che 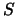 deve essere uno scalare, dato che le equazioni del moto derivano
dalla condizione di estremo su di essa.
deve essere uno scalare, dato che le equazioni del moto derivano
dalla condizione di estremo su di essa.
Con l'assunto che l'azione sia invariante, dalla (1.96)
siamo allora in grado di ricavare le proprietà di trasformazione della
lagrangiana 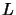 ; introducendo
; introducendo
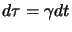 infatti otteniamo che:
infatti otteniamo che:
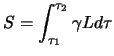 |
(2.98) |
e siccome  è invariante otteniamo che lo è pure
è invariante otteniamo che lo è pure  ; adesso se
vogliamo ottenere la lagrangiana di una particella libera ancora una volta, per
l'omogeneità dello spazio-tempo questo non potrà dipendere dalle coordinate, ma
solo dalla velocità, ma l'unica funzione invariante della quadrivelocità è
; adesso se
vogliamo ottenere la lagrangiana di una particella libera ancora una volta, per
l'omogeneità dello spazio-tempo questo non potrà dipendere dalle coordinate, ma
solo dalla velocità, ma l'unica funzione invariante della quadrivelocità è
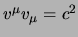 , per cui alla fine avremo che:
il confronto col precedente limite classico determina
, per cui alla fine avremo che:
il confronto col precedente limite classico determina 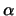 e ci da:
e ci da:
 |
(2.99) |
e si può verificare che questa, con le
(1.97), da la corretta equazione del moto
per una particella libera:
inoltre si può verificare che con questa lagrangiana si riottengono i
valori dell'impulso e dell'energia trovati al
§1.3.1 con le definizioni:
Dalla (1.99) si può inoltre ottenere
l'espressione dell'azione per una particella libera; sostituendo nella
(1.98) si ha:
Resta però aperto il problema di esprimere le equazioni del moto in forma
covariante a vista, e di ottenere il quadrimpulso come un opportuno momento
coniugato.
Un modo per farlo è introdurre come lagrangiana relativistica invariante:
che a questo punto viene pensata funzione delle coordinate  e della
quadrivelocità
e della
quadrivelocità 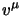 , cioè
, cioè
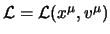 ; l'azione allora
si esprime come:
; l'azione allora
si esprime come:
 |
(2.100) |
ed un'estensione covariante a vista delle
(1.97) può essere:
 |
(2.101) |
ottenere questa però è tutt'altro che banale; si noti anzitutto che queste
sono, nel caso di una particella, quattro equazioni contro le tre precedenti;
il problema è che se usa la (1.100) col caso noto di una
particella libera per la quale:
quando si va a fare il calcolo variazionale per avere l'equazione del moto si
deve tenere conto del vincolo
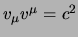 , che equivalentemente si può
esprimere come:
per cui non tutte le componenti della (1.101) sono
indipendenti.
, che equivalentemente si può
esprimere come:
per cui non tutte le componenti della (1.101) sono
indipendenti.
Una forma equivalente della (1.101) si può ottenere
esprimendo la (1.100) in funzione di 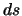 (che nel caso di una
particella libera ci dice semplicemente che per il principio di minima azione
una particella in moto tende a seguire le geodetiche) in tal caso applicando
il principio variazionale si ha:
(che nel caso di una
particella libera ci dice semplicemente che per il principio di minima azione
una particella in moto tende a seguire le geodetiche) in tal caso applicando
il principio variazionale si ha:
dove
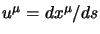 .
Infine si può ottenere l'espressione del quadrimpulso come momento coniugato se
prendiamo:
.
Infine si può ottenere l'espressione del quadrimpulso come momento coniugato se
prendiamo:




Next: Formulazione lagrangiana del moto
Up: Formulazione lagrangiana
Previous: Formulazione lagrangiana
Contents
Index
Simone Piccardi
2003-02-20
![]() , che in generale è funzione solo delle
coordinate
, che in generale è funzione solo delle
coordinate ![]() e delle loro derivate
e delle loro derivate ![]() (il moto è completamente
determinato dalla posizione e dalla velocità iniziale) come:
(il moto è completamente
determinato dalla posizione e dalla velocità iniziale) come:

![]() deve essere uno scalare, dato che le equazioni del moto derivano
dalla condizione di estremo su di essa.
deve essere uno scalare, dato che le equazioni del moto derivano
dalla condizione di estremo su di essa.
![]() ; introducendo
; introducendo
![]() infatti otteniamo che:
infatti otteniamo che:

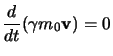
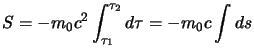
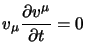
![]() (che nel caso di una
particella libera ci dice semplicemente che per il principio di minima azione
una particella in moto tende a seguire le geodetiche) in tal caso applicando
il principio variazionale si ha:
(che nel caso di una
particella libera ci dice semplicemente che per il principio di minima azione
una particella in moto tende a seguire le geodetiche) in tal caso applicando
il principio variazionale si ha:
