




Next: Il propagatore in meccanica
Up: Il propagatore classico
Previous: Lo sviluppo perturbativo
Contents
Index
La trasformata di Fourier del propagatore
La soluzione dell'equazione differenziale per il propagatore è in genere più
semplice se si usano le trasformate di Fourier, in tal caso infatti le
equazioni che contengono operatori di derivazione possono essere trasformate
in semplici equazioni algebriche.
Il primo passo da fare è osservare che siccome tutti i problemi fisici di una
qualche rilevanza presentano invarianza di traslazione, il propagatore quindi
non sarà mai funzione di 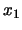 e
e  separatamente, ma solo della differenza
separatamente, ma solo della differenza
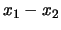 . Questo ci permette di scriverne la trasformata di Fourier in
maniera assolutamente generale come:
. Questo ci permette di scriverne la trasformata di Fourier in
maniera assolutamente generale come:
 |
(4.12) |
nel caso dell'equazione di Schroedinger per una particella libera l'equazione
che otteniamo è:
adesso possiamo usare la rappresentazione della delta di Dirac:
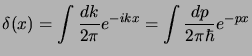 |
(4.13) |
per cui la precedente diventa:
dalla quale, portando le derivate dentro l'integrale, si
ottiene4.4 l'equazione algebrica:
questo ci mostra che per
 si ha:
si ha:
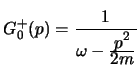 |
(4.14) |
il problema che sorge qui è che questa è ovviamente una funzione singolare;
d'altra parte per
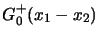 non si ha solo l'equazione
(3.5), ma anche la condizione al contorno che sia
non si ha solo l'equazione
(3.5), ma anche la condizione al contorno che sia
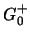 nulla per
nulla per 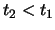 ; allora è il comportamento nella singolarità che ci
darà l'andamento delle condizioni al contorno.
; allora è il comportamento nella singolarità che ci
darà l'andamento delle condizioni al contorno.
Figure:
I due cammini su cui si applica il Lemma di Jordan per il calcolo
dell'integrale del propagatore  usando l'espressione
(3.15) di
usando l'espressione
(3.15) di 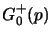 nello spazio degli
impulsi.
nello spazio degli
impulsi.
|
|
Il trucco per risolvere il problema, che permette integrare la
(3.12) con questa espressione singolare per 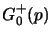 ed ottenere al contempo le condizioni al contorno, è quello di aggiungere a
denominatore della
ed ottenere al contempo le condizioni al contorno, è quello di aggiungere a
denominatore della 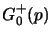 una quantità complessa infinitesimale
una quantità complessa infinitesimale
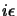 che sposta il polo dall'asse reale e permette di calcolare
l'integrale; esprimeremo cioè il propagatore nello spazio degli impulsi come:
che sposta il polo dall'asse reale e permette di calcolare
l'integrale; esprimeremo cioè il propagatore nello spazio degli impulsi come:
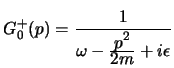 |
(4.15) |
(dove si è sottinteso un
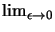 da aggiungere a questa
espressione tutte le volte che la si integra) con la quale l'equazione per il
propagatore diventa:
per questo integrale possiamo usare il lemma di Jordan, calcolando
l'integrale su un cammino chiuso nel piano complesso. Per farlo consideriamo i
due cammini illustrati in fig. 3.2, costituiti dall'asse reale
chiuso da un semicerchio all'infinito. Adesso se
da aggiungere a questa
espressione tutte le volte che la si integra) con la quale l'equazione per il
propagatore diventa:
per questo integrale possiamo usare il lemma di Jordan, calcolando
l'integrale su un cammino chiuso nel piano complesso. Per farlo consideriamo i
due cammini illustrati in fig. 3.2, costituiti dall'asse reale
chiuso da un semicerchio all'infinito. Adesso se 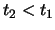 l'esponenziale va a
zero per
l'esponenziale va a
zero per
 , quindi usando il cammino chiuso nel semipiano
superiore, che non contiene poli, otterremo che il risultato, per il teorema
dei residui, è zero. Se viceversa
, quindi usando il cammino chiuso nel semipiano
superiore, che non contiene poli, otterremo che il risultato, per il teorema
dei residui, è zero. Se viceversa 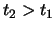 perché l'esponenziale si annulli
deve essere
perché l'esponenziale si annulli
deve essere
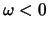 e dobbiamo usare il cammino chiuso nel semipiano
inferiore; si ottiene così che:
(essendo il cammino che da l'integrale in senso antiorario si è cambiato
segno); questo si risolve banalmente tenendo conto che per poli del primo
ordine come questo si ha che:
dunque:
per cui alla fine si ottiene che:
e se consideriamo che le soluzioni per l'equazione di Schroedinger di
particella libera sono:
si vede subito che questa è proprio nella forma4.5 della (3.8).
e dobbiamo usare il cammino chiuso nel semipiano
inferiore; si ottiene così che:
(essendo il cammino che da l'integrale in senso antiorario si è cambiato
segno); questo si risolve banalmente tenendo conto che per poli del primo
ordine come questo si ha che:
dunque:
per cui alla fine si ottiene che:
e se consideriamo che le soluzioni per l'equazione di Schroedinger di
particella libera sono:
si vede subito che questa è proprio nella forma4.5 della (3.8).
Come si vede la prescrizione di aggiungere un 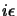 al denominatore
dell'espressione (3.15) ci permette di
ottenere la condizione al contorno che volevamo, questo è quanto ci aspettiamo
se consideriamo che una delle possibili definizioni della funzione
al denominatore
dell'espressione (3.15) ci permette di
ottenere la condizione al contorno che volevamo, questo è quanto ci aspettiamo
se consideriamo che una delle possibili definizioni della funzione 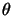 è:
è:
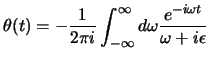 |
(4.16) |
che, calcolando l'integrale con lo stesso procedimento appena mostrato per
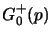 , che ha esattamente la stessa forma, ci dà la definizione vista in
(2.109).
, che ha esattamente la stessa forma, ci dà la definizione vista in
(2.109).
Da questa definizione si ottiene anche la relazione
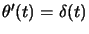 usata per dimostrare la (3.5) all'inizio del capitolo,
basta osservare infatti che:
usata per dimostrare la (3.5) all'inizio del capitolo,
basta osservare infatti che:
dove si è effettuato l'ultimo passaggio semplificando
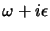 con
con  .
.





Next: Il propagatore in meccanica
Up: Il propagatore classico
Previous: Lo sviluppo perturbativo
Contents
Index
Simone Piccardi
2003-02-20
![]() e
e ![]() separatamente, ma solo della differenza
separatamente, ma solo della differenza
![]() . Questo ci permette di scriverne la trasformata di Fourier in
maniera assolutamente generale come:
. Questo ci permette di scriverne la trasformata di Fourier in
maniera assolutamente generale come:
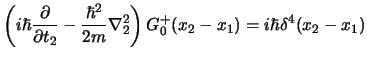
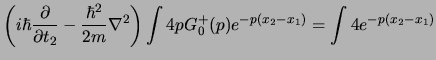

![\includegraphics[width=14cm]{fig_4_2}](img1442.png)
![]() ed ottenere al contempo le condizioni al contorno, è quello di aggiungere a
denominatore della
ed ottenere al contempo le condizioni al contorno, è quello di aggiungere a
denominatore della ![]() una quantità complessa infinitesimale
una quantità complessa infinitesimale
![]() che sposta il polo dall'asse reale e permette di calcolare
l'integrale; esprimeremo cioè il propagatore nello spazio degli impulsi come:
che sposta il polo dall'asse reale e permette di calcolare
l'integrale; esprimeremo cioè il propagatore nello spazio degli impulsi come:
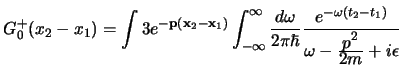
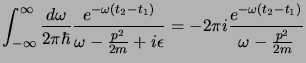
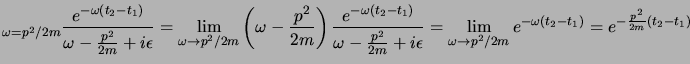
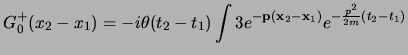
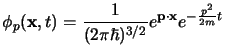
![]() al denominatore
dell'espressione (3.15) ci permette di
ottenere la condizione al contorno che volevamo, questo è quanto ci aspettiamo
se consideriamo che una delle possibili definizioni della funzione
al denominatore
dell'espressione (3.15) ci permette di
ottenere la condizione al contorno che volevamo, questo è quanto ci aspettiamo
se consideriamo che una delle possibili definizioni della funzione ![]() è:
è:
![]() usata per dimostrare la (3.5) all'inizio del capitolo,
basta osservare infatti che:
usata per dimostrare la (3.5) all'inizio del capitolo,
basta osservare infatti che: