Il limite classico dell'equazione di Dirac

Per capire se questa equazione ha davvero un significato fisico vogliamo verificare cosa diventa al limite non relativistico; in questo caso $v\ll c$ per cui nella (2.9) in $H$ il termine $c\bf p$ è trascurabile e l'equazione diventa:

$$i\hbar {\partial{\psi}\over \partial t}= m c^2\beta\psi$$

(che è valida esattamente solo per $v = 0$) adesso l'equazione si risolve banalmente perché nella rappresentazione (2.13) $\beta$ è diagonale e si ha:

$$\psi_1=e^{-i{\scriptstyle mc^2\over \scriptstyle\hbar}t} \begin{p... ...\over \scriptstyle\hbar}t} \begin{pmatrix} 0\cr 0\cr 0\cr 1\cr \end{pmatrix}$$

e qui salta fuori la magagna, infatti le prime due van bene, ma le altre due no poiché sono soluzioni ad energia negativa, e ci si ritrova con lo stesso problema dell'equazione di Klein-Gordon.

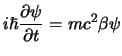
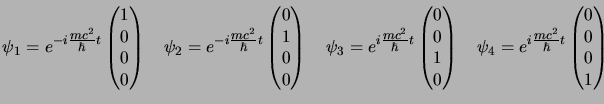
In questo caso però l'interpretazione probabilistica, dato che $\rho$ è ancora definita positiva, non viene meno; inoltre l'equazione lascia intravedere alcuni sviluppi estremamente significativi; infatti se cancelliamo le componenti relative alle soluzioni ad energia negativa vediamo che $\psi_1$ e $\psi_2$ sono identici agli autostati di una particella di spin $1/2$, suggerendo la possibilità di ottenere lo spin, introdotto ad hoc in meccanica quantistica, direttamente dalla relatività, senza doverlo più postulare come caratteristica intrinseca della particella.

Per verificare tale possibilità Dirac accantonò sul momento il problema delle soluzioni ad energia negativa, per vedere cosa succede quando si aggiunge l'interazione elettromagnetica; la prima cosa fu riscriversi $\psi$ nei termini di quelle che sono chiamate rispettivamente grande e piccola componente ($\varphi$ e $\chi$) come:

$$\psi= \begin{pmatrix} \varphi\cr \chi\cr \end{pmatrix}$$

dove evidentemente $\chi$ e $\varphi$ sono spinori $2 \times 1$; poi introduciamo l'interazione elettromagnetica con la sostituzione minimale (vedremo i dettagli in §2.5.1) per cui la (2.9) diventa:

$$i\hbar {\partial{\psi}\over \partial t}= \left[ c \boldsymbol{\alpha} (-i\hbar\nabla-\ec {\bf A})+ m c^2\beta +e\phi\right]\psi$$ (3.14)

allora se prendiamo il momento coniugato:

$$\boldsymbol{\pi}=-i\hbar\nabla-\ec {\bf A}$$

si può riscrivere la (2.14) nei termini delle componenti $\chi$ e $\varphi$ come sistema di equazioni accoppiate: usando la definizione e la rappresentazione (2.13) che abbiamo trovato per le nostre matrici otteniamo che:

$$\begin{aligned} i\hbar {\partial{\varphi}\over \partial t}&... ...\cdot\boldsymbol{\pi})\varphi+ e\phi\chi-mc^2\chi \end{aligned}$$

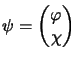
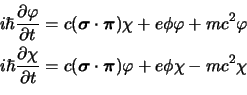
Nel caso non relativistico il termine principale è quello in $mc^2$, e queste si semplificano introducendo la variazione temporale principale negli spinori e prendendo i nuovi:

$$\begin{aligned} \Phi&=e^{-i{\scriptstyle mc^2\over \scriptst... ...{\scriptstyle mc^2\over \scriptstyle \hbar}t}\chi \end{aligned}$$

che sostituiti nella precedente danno:

adesso nella seconda si può introdurre l'approssimazione non relativistica per piccoli valori dell'energia cinetica e del potenziale^3.1, trascurando tutti i termini in $\Psi$, che è la piccola componente, tranne quello in $mc^2$, si ottiene:

$$\Psi={\boldsymbol{\sigma}\cdot\boldsymbol{\pi}\over 2mc}\Phi$$

per cui la prima delle (2.15) ci da l'equazione finale per $\Phi$:

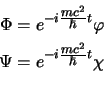
$$i\hbar {\partial{\Phi}\over \partial t}=\left[{ (\boldsymbol{\sig... ...ol{\pi}) (\boldsymbol{\sigma}\cdot\boldsymbol{\pi})\over 2m} +e\phi\right]\Phi$$

e da questa, sfruttando l'identità:

$$(\boldsymbol{\sigma}\cdot{\bf a}) (\boldsymbol{\sigma}\cdot{\bf b})= {\bf a}\cdot {\bf b}+ i\boldsymbol{\sigma}\cdot({\bf a}\times {\bf b})$$

si ottiene che:

$$(\boldsymbol{\sigma}\cdot\boldsymbol{\pi}) (\boldsymbol{\sigma}\c... ...mbol{\pi}^2+ i\boldsymbol{\sigma}\cdot(\boldsymbol{\pi}\times\boldsymbol{\pi})$$

ma dalla definizione:

$$i\boldsymbol{\sigma}\cdot( \boldsymbol{\pi}\times\boldsymbol{\pi}... ...ar\nabla-\ec {\bf A}\right]={e\hbar\over c} \boldsymbol{\sigma}\cdot {\bf B}$$

dunque alla fine l'equazione diventa:

$$i\hbar {\partial{\Phi}\over \partial t}= \left[{({\bf p}-(e/c){\b... ...ver 2m} -{e\hbar\over 2mc} \boldsymbol{\sigma}\cdot {\bf B} +e\phi \right]\Phi$$

che è esattamente l'equazione di Pauli, con lo spin dell'elettrone. Si noti anche che l'interazione dello spin col campo magnetico ha la forma:

$$H_{\rm inter}= -{e\hbar\over 2mc} \boldsymbol{\sigma}\cdot {\bf B} =\boldsymbol{\mu} \cdot {\bf B}$$

dove si è definito il momento magnetico $\boldsymbol{\mu}$ come:

$$\boldsymbol{\mu}= {e\hbar\over 2mc} \boldsymbol{\sigma}= 2\left({e\hbar\over 2mc}\right) {\boldsymbol{\sigma}\over 2}= 2\mu_B {\bf s}$$

dove s definito dalla relazione che esprime l'operatore di spin ${\bf S}=\boldsymbol{\sigma}/2=\hbar {\bf s}$ (è cioè lo spin in unità $\hbar$) mentre:

$$\mu_B={e\hbar\over 2mc}$$ (3.16)

è il magnetone di Bohr.

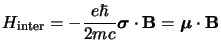
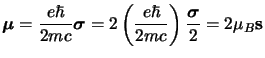
Nella meccanica classica l'interazione di una carica in moto circolare col campo magnetico è descritta da una energia di interazione del tipo:

$$H={e\over 2mc} {\bf L \cdot B}$$ (3.17)

con L momento angolare orbitale; questa in meccanica quantistica classica resta uguale solo che si usa l'operatore di momento angolare orbitale ${\bf L}= \hbar {\bf l}$; l'interazione perciò è ancora nella forma della (2.17) con $\boldsymbol{\mu}= \mu_B {\bf l}$.

Nel nostro caso troviamo che l'elettrone ha una ulteriore interazione di tipo momento angolare, dovuta alla presenza del termine dello spin, ma il momento magnetico è il doppio del valore che si ottiene nella meccanica quantistica classica; dall'equazione di Dirac dunque si ottiene non solo lo spin dell'elettrone, ma anche il corretto valore del rapporto giromagnetico $g$ definito dalla relazione:

$$\boldsymbol{\mu}= g \mu_B {\bf j}$$

che risulta appunto essere $g=2$, come risulta sperimentalmente, ma che nella teoria di Pauli era stato introdotto ad hoc, insieme allo spin, per poter spiegare i risultati sperimentali.

Il fatto che l'equazione di Dirac riuscisse ad ottenere tutti questi risultati con la semplice richiesta di invarianza relativistica fece si che i problemi che avevano portato all'abbandono dell'equazione di Klein-Gordon venissero in un primo tempo accantonati prima che Dirac, spinto dal successo ottenuto, risolvesse la questione introducendo l'esistenza dell'antimateria.