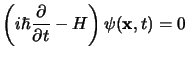Definizione ed equazioni fondamentali

Cominciamo con il richiamare brevemente la costruzione della teoria del propagatore in meccanica quantistica classica, vedremo poi (in sez. 3.2) come, con una estensione immediata e naturale, è possibile passare alla meccanica quantistica relativistica.

Nella meccanica quantistica classica l'evoluzione del moto di un sistema è governata dall'equazione di Schroedinger:

$$\left (i \hbar {\partial{}\over \partial t} - H \right) \psi({\bf x},t) = 0$$ (4.1)

questa è un'equazione omogenea al primo ordine in $t$ e sappiamo che per tali equazioni nota una soluzione qualsiasi $\psi$ al tempo $t$ si può determinare univocamente la soluzione al tempo $t'$. Si può dimostrare che questo è equivalente a dire che si può sempre scrivere:

$$\psi({\bf x'},t') = \int d^3 x\, G({\bf x'},t';{\bf x},t)\psi({\bf x},t)$$ (4.2)

dove $G({\bf x'},t';{\bf x},t)$ è una opportuna funzione che viene chiamata funzione di Green.

La funzione di Green in questa forma in genere però non viene usata, se infatti va bene per la matematica, per la fisica occorre anche tenere presente il principio di causalità. Siccome $G({\bf x'},t';{\bf x},t)$ esprime la dinamica del sistema, se in $H$ c'è una un'interazione che inizia ad un certo istante $t_0$ esso impone che i suoi effetti non possano essere sentiti prima dell'azione della forza; in sostanza in fisica si vuole che la (3.2) valga solo per $t'>t$; per questo si usa il propagatore, detto anche funzione di Green ritardata, definito^4.1 come:

$$G^+({\bf x'},t';{\bf x},t) = \theta(t'-t) G({\bf x'},t';{\bf x},t... ...x{per $t^\prime \ge t$} \cr \qquad 0 & \hbox{per $t^\prime <t$} \cr \end{cases}$$ (4.3)

per il quale è immediato, usando la (3.2), verificare che vale la relazione:

$$\theta(t'-t)\psi({\bf x'},t') = \int d^3x G^+({\bf x'},t';{\bf x},t)\psi({\bf x},t)$$ (4.4)

e questa che è l'equazione integrale che definisce $G^+$.

E' però molto più utile poter disporre di una relazione differenziale, che in genere è il punto di partenza in cui in matematica si definisce la funzione di Green, si è preferito partire dalle relazioni precedenti per far capire meglio il senso fisico di ciò di cui si sta parlando; se applichiamo l'operatore differenziale definito nell'equazione di Schroedinger alla soluzione ottenuta con il propagatore avremo:

$$\left( i\hbar {\partial\over\partial t'} - H' \right) \theta(t'-... ...artial\over\partial t'} - H' \right) G^+({\bf x'},t';{\bf x},t)\psi({\bf x},t)$$

adesso a primo membro possiamo sempre considerare che $H' \theta(t'-t) = \theta(t'-t)H'$ in quanto al più $H'$ può essere un operatore che dipende dal tempo, non che opera sul tempo, pertanto il prodotto è comunque commutativo; pertanto se sviluppiamo otterremo:

$$\left( i\hbar{\partial\over\partial t'} - H' \right) \theta(t'... ...-t) \left( i\hbar{\partial\over\partial t'} - H' \right) \psi({\bf x'},t')$$

adesso qui il secondo addendo è nullo perché $\psi({\bf x}',t')$ è soluzione della (3.1), inoltre, come già detto, e come dimostraremo in (3.17), la derivata della $\theta(t'-t)$ porta ad una delta di Dirac e quello che resta è:

$$i\hbar\delta(t'-t) \psi({\bf x'},t')$$

dunque si ha:

$$i\hbar\delta(t'-t) \psi({\bf x'},t') = \int d^3x \left( i\hbar{\partial{}\over \partial t}-H \right) G^+({\bf x'},t';{\bf x},t) \psi({\bf x},t)$$

e perché questa sia verificata occorre che l'integrale ci riporti il primo membro, il che richiede che sia:

$$\left( i\hbar{\partial{}\over \partial t}-H \right) G^+({\bf x'},t';{\bf x},t) = i\hbar\delta(t'-t)\delta^3({\bf x'}-{\bf x})$$

per cui in definitiva (adottiamo per semplicità la notazione $x=({\bf x},t)$) si ottiene l'equazione differenziale del propagatore:

$$\left( i\hbar{\partial{}\over \partial t}-H \right) G^+(x', x) = i\hbar\delta^4(x'-x)$$ (4.5)

a cui va aggiunta, per completezza, la condizione al contorno che $G^+(x', x)$ sia nullo per $t'<t$.

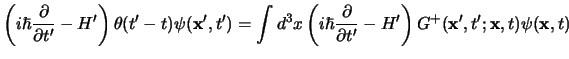
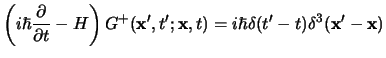
Fin qui nient'altro che la definizione, ma se la questione fosse solo quella di passare dalla ricerca di soluzioni della (3.1) a quelle della (3.5) avremmo ottenuto ben poco, infatti quest'ultima, essendo un'equazione non omogenea con una distribuzione, è sicuramente assai più rognosa della precedente, e la conoscenza di $G^+$ porta semplicemente una trattazione equivalente.

Infatti se sono note le soluzioni della (3.1) si può sempre costruire la funzione di Green. Per semplicità prendiamo una hamiltoniana time-independent e con spettro discreto;^4.2 risolvere l'equazione vuol dire trovare una base nello spazio di Hilbert delle funzioni d'onda costituita da autovettori dell'hamiltoniana $H$ nella forma:

$$\phi_n({\bf x},t)=u_n({\bf x}) e^{-\ih E_n t}$$ (4.6)

dove le $u_n({\bf x})$ obbediscono alle relazioni:

$$\int d^3x\, u_i({\bf x})u_j({\bf x}) = \delta_{ij} \qquad\hbox{e}\qquad \sum_n u_n^*({\bf x}) u_n({\bf x}) = \delta^3(x)$$

che esprimono rispettivamente le proprietà di ortonormalità e completezza della base; in questo modo una soluzione qualunque della (3.1) si potrà sempre esprimere come:

$$\psi({\bf x},t) = \sum_n c_n \phi_n({\bf x},t)$$

dove i $c_n$ sono dei fattori costanti.

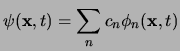
Allora, supposto di aver determinato le soluzioni, possiamo verificare che se prendiamo come funzione di Green l'espressione:

$$G({\bf x'},t';{\bf x},t) = \sum_n u_n({\bf x'}) e^{-\ih E_n t'} u... ...\bf x}) e^{\ih E_n t} = \sum_n u_n({\bf x'}) u^*_n({\bf x}) e^{-\ih E_n (t'-t)}$$ (4.7)

questa soddisfa, per le suddette proprietà di ortonormalità e completezza, la (3.2). Infatti avremo, sostituendo a secondo membro le espressioni (3.6) e (3.7), che:

$$\begin{aligned} \int d^3x\, & \sum_n u_n({\bf x'}) u^*_n(... ...\bf x'}) e^{-\ih E_n t'} = \psi({\bf x'}, t') \cr \end{aligned}$$

che è appunto la (3.2).

Dalla (3.7) è immediato ottenere anche l'espressione per il propagatore, che, seguendo la definizione (3.3), è:

$$G^+({\bf x'},t';{\bf x},t) = \begin{cases}\sum_n u_n({\bf x'}) u^... ...per $t^\prime \ge t$}\cr \qquad\qquad0&\hbox{per $t^\prime <t$} \cr \end{cases}$$ (4.8)