Lo sviluppo perturbativo

Il vantaggio nell'uso del propagatore rispetto alla soluzione classica dell'equazione di Schroedinger sta nel fatto che esso si presta ad una trattazione molto elegante ed utile dei problemi di scattering con la teoria perturbativa, che continua a valere anche nell'estensione relativistica.

Se infatti conosciamo la soluzione di un problema semplice di hamiltoniana $H_0$, per il quale il propagatore $G^+_0$ è noto,^4.3 una volta che aggiungiamo una interazione $V(x)$ avremo per $G^+$ l'equazione:

$$\left( i\hbar{\partial{}\over \partial t}-H_0-V \right) G^+({\bf x'},t';{\bf x},t) = i\hbar\delta(t'-t)\delta^3({\bf x'}-{\bf x})$$ (4.9)

con la condizione al contorno che sia $G^+({\bf x'},t';{\bf x},t)=0$ se $t'<t$. Quello che si ottiene è che una soluzione di questa equazione si può sempre scrivere nella forma (adottando una volta per tutte la notazione quadrivettoriale):

$$G^+(x_2;x_1) = G_0^+(x_2;x_1) + \left( 1 \over i \hbar \right) \int d^4x_3 G_0^+(x_2;x_3) V(x_3) G^+(x_3;x_1)$$ (4.10)

Per dimostrarlo possiamo sfruttare un teorema che dice che equazioni come la (3.9) hanno una soluzione unica; allora se verifichiamo che effettivamente la (3.10) la soddisfa e soddisfa pure la condizione al contorno siamo a posto; applichiamo allora a quest'ultima la parte imperturbata dell'operatore differenziale; otteniamo:

$$\begin{aligned} \left( i\hbar{\partial{}\over \partial t}-H... ... [i\hbar\delta^4(x_2-x_3)] V(x_3) G^+(x_3;x_1)\cr \end{aligned}$$

dove si è usata la definizione di $G_0^+$; da questa è immediato ottenere:

$$\left( i\hbar{\partial{}\over \partial t}-H_0 \right)G^+(x_2;x_1) = i\hbar\delta^4(x_2-x_1)+V(x_2) G^+(x_2;x_1)$$

che è banalmente la (3.9); adesso resta da vedere la condizione al contorno; se $t_2<t_1$ ovviamente $G_0^+(x_2;x_1)=0$ per cui resta:

$$G^+(x_2;x_1) = \left( 1\over i\hbar \right) \int d^4x_3 G_0^+(x_2;x_3) V(x_3) G^+(x_3;x_1)$$

qui non è detto che sia sempre $G_0^+(x_2; x_3)=0$ dato che può essere $t_2>t_3$, ma è evidente che se prendiamo $G^+(x_2; x_1)=0$ per $t_2<t_1$ questa equazione è soddisfatta (dato che per $t_2>t_3$ è nulla $G^+$ poiché $t_3<t_2<t_1$ e per il resto è nulla $G_0$). Quindi $G^+(x_2; x_1)=0$ per $t_2>t_1$ è una soluzione possibile e dato che tutto è consistente e la soluzione è unica siamo a posto.

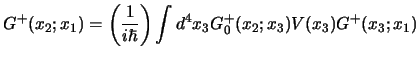
La (3.10) è la formula fondamentale che permette di sviluppare con la teoria del propagatore il calcolo perturbativo; infatti utilizzandola per $G^+(x_2;x_1)$ dentro l'integrale a secondo membro si ottiene:

$$\begin{aligned} G^+(x_2;x_1) &= G_0^+(x_2;x_1) + \cr &+ \... ...;x_3) V(x_3) G_0^+(x_3;x_4)V(x_4) G^+(x_4;x_1)\cr \end{aligned}$$

ed allora, iterando la sostituzione, si può ottenere:

$$\begin{aligned}G^+(x';x) &= G_0^+(x';x) + \sum_{n=1}^\infty \... ...x_{n-1}) G_0^+(x_{n-1};x_n)V(x_n) G_0^+(x_n;x)\cr \end{aligned}$$

che è lo sviluppo perturbativo che cercavamo.

Figure 3.1: Interpretazione fisica dello sviluppo perturbativo del propagatore, in termini di somme su propagazioni libere e interazioni; in figura sono rappresentati i primi tre termini (si noti come i tempi siano ordinati in modo crescente.

Questa ultima formula ha una interessante interpretazione in termini che assomigliano a quelli che in modo più elaborato saranno i diagrammi di Feynmann; se guardiamo in fig. 3.1 tenendo presente la (3.11) possiamo vedere come si costruisca il propagatore esatto come somma dei vari termini in approssimazioni successive; il primo è banalmente il propagatore libero che porta direttamente da $x_i=({\bf x}_i,t_i)$ a $x_f=({\bf x}_f,t_f)$ senza considerare l'interazione; il secondo è la prima correzione che si costruisce con una propagazione libera fino al punto intermedio $x_1=({\bf x}_1,t_1)$ dove si aggiunge l'interazione col potenziale per poi proseguire col propagatore libero fino al punto finale, integrando su tutti i possibili punti intermedi. Allo stesso modo, usando due interazioni intermedie, si effettua la correzione del secondo ordine, e analogamente per i termini successivi; si noti poi che l'uso del propagatore $G^+$ ci evita di dover imporre nelle integrazioni che i tempi siano posti in sequenza crescente, come nella figura, per tener conto della causalità.