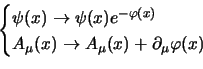



Next: La teoria di Dirac
Up: L'interazione col campo elettromagnetico
Previous: L'interazione col campo elettromagnetico
Contents
Index
L'interazione minimale
Ci limiteremo per adesso ad introdurre l'interazione col campo
elettromagnetico come interazione con un campo esterno, abbiamo esaminato la
teoria relativistica dell'interazione di una particella col campo
elettromagnetico al §1.6.1, ed abbiamo visto come
per una particella di carica 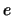 in interazione con un potenziale
elettromagnetico
in interazione con un potenziale
elettromagnetico 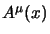 il momento coniugato fosse:
il momento coniugato fosse:
 |
(3.113) |
questa è la cosiddetta interazione minimale, ed è la forma più
semplice di schematizzazione dell'interazione del campo elettromagnetico con
una particella puntiforme; si noti anche che inserendo 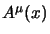 come campo
esterno dato si trascurano ad esempio gli effetti dovuti alla presenza della
particella carica in interazione.
come campo
esterno dato si trascurano ad esempio gli effetti dovuti alla presenza della
particella carica in interazione.
La (2.113) ci permette di effettuare la quantizzazione
con la (2.4), ma adesso 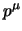 non è più
l'operatore corrispondente alla quantità di moto cinetica della particella, e
quindi non potremo usare la relazione
non è più
l'operatore corrispondente alla quantità di moto cinetica della particella, e
quindi non potremo usare la relazione
 (che deriva dalla
relazione relativistica
(che deriva dalla
relazione relativistica
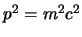 ) che ci aveva permesso di scrivere
l'equazione di Dirac per la particella libera, però questa varrà ancora per la
parte cinetica del momento coniugato, allora se prendiamo:
) che ci aveva permesso di scrivere
l'equazione di Dirac per la particella libera, però questa varrà ancora per la
parte cinetica del momento coniugato, allora se prendiamo:
per questo sarà ancora
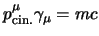 e quindi potremo
scrivere l'equazione di Dirac nella forma:
che in forma compatta è:
e quindi potremo
scrivere l'equazione di Dirac nella forma:
che in forma compatta è:
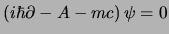 |
(3.114) |
L'invarianza di Lorentz di questa equazione, evidente a vista dato che
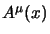 è un quadrivettore, si dimostra con l'esatto identico procedimento
dello scorso capitolo, dato che
è un quadrivettore, si dimostra con l'esatto identico procedimento
dello scorso capitolo, dato che  trasforma esattamente come
trasforma esattamente come
 per cui in quanto visto al §2.3.2 basta sostituire a
quest'ultimo
per cui in quanto visto al §2.3.2 basta sostituire a
quest'ultimo
 .
.
Da questa poi si può ottenere l'analoga per l'aggiunto; come per l'equazione
libera si prende la coniugata hermitiana della (2.114):
(evidentemente 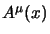 è reale e la coniugazione non gli fa nulla), qui
si opera come al §2.3.4 usando l'espressione nota per
è reale e la coniugazione non gli fa nulla), qui
si opera come al §2.3.4 usando l'espressione nota per
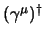 , e moltiplicando questa per
, e moltiplicando questa per 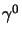 a destra (e
cambiando segno) si ottiene:
che si riscrive anche come:
a destra (e
cambiando segno) si ottiene:
che si riscrive anche come:
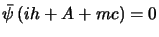 |
(3.115) |
dove con  si intende che le derivate devono essere applicate allo
spinore a sinistra, mentre con
si intende che le derivate devono essere applicate allo
spinore a sinistra, mentre con  intenderemo la stessa cosa ma per lo
spinore a destra (cioè le derivate standard, contenute ad esempio nella
(2.114)).
intenderemo la stessa cosa ma per lo
spinore a destra (cioè le derivate standard, contenute ad esempio nella
(2.114)).
Con l'equazione per l'aggiunto possiamo ricavare la quadricorrente col solito
procedimento, si moltiplica la (2.115) a destra per 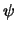 e la
(2.114) a sinistra per
e la
(2.114) a sinistra per  e si sommano, in questo modo i
termini nel potenziale e in
e si sommano, in questo modo i
termini nel potenziale e in  se ne vanno e resta solo:
se ne vanno e resta solo:
dunque si riottiene la conservazione della quadricorrente
 che è esattamente la stessa del caso di
particella libera.
che è esattamente la stessa del caso di
particella libera.
Quella che invece deve essere verificata è l'invarianza di gauge, bisogna
infatti ricordarsi che  è sempre definito a meno di una
trasformazione di gauge, per cui se prendiamo un altro potenziale:
è sempre definito a meno di una
trasformazione di gauge, per cui se prendiamo un altro potenziale:
(con
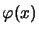 funzione qualsiasi) questo deve dare gli stessi risultati
fisici del precedente. Usando
funzione qualsiasi) questo deve dare gli stessi risultati
fisici del precedente. Usando 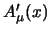 l'equazione di Dirac diventa:
adesso si tratta di trovare
l'equazione di Dirac diventa:
adesso si tratta di trovare 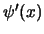 a partire da
a partire da 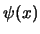 , allora
osserviamo che se prendiamo:
, allora
osserviamo che se prendiamo:
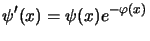 |
(3.116) |
si vede subito che:
per cui la precedente diventa:
che si riduce immediatamente a:
dunque la (2.116) è ancora soluzione
dell'equazione di Dirac. Inoltre è banale verificare che anche la
quadricorrente è invariante giacché il fattore di fase acquisito da 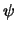 viene annullato da quello, opposto, acquisito da
viene annullato da quello, opposto, acquisito da  . Questo ci dice
anche, dato che tutte le quantità fisiche si possono esprimere tramite le
forme bilineari del tipo
. Questo ci dice
anche, dato che tutte le quantità fisiche si possono esprimere tramite le
forme bilineari del tipo
 viste in
§2.3.6 che l'invarianza di gauge è dimostrata in
generale, e che le trasformazioni di gauge del sistema campo
elettromagnetico/spinore sono date da:
viste in
§2.3.6 che l'invarianza di gauge è dimostrata in
generale, e che le trasformazioni di gauge del sistema campo
elettromagnetico/spinore sono date da:




Next: La teoria di Dirac
Up: L'interazione col campo elettromagnetico
Previous: L'interazione col campo elettromagnetico
Contents
Index
Simone Piccardi
2003-02-20
![]() in interazione con un potenziale
elettromagnetico
in interazione con un potenziale
elettromagnetico ![]() il momento coniugato fosse:
il momento coniugato fosse:
![]() non è più
l'operatore corrispondente alla quantità di moto cinetica della particella, e
quindi non potremo usare la relazione
non è più
l'operatore corrispondente alla quantità di moto cinetica della particella, e
quindi non potremo usare la relazione
![]() (che deriva dalla
relazione relativistica
(che deriva dalla
relazione relativistica
![]() ) che ci aveva permesso di scrivere
l'equazione di Dirac per la particella libera, però questa varrà ancora per la
parte cinetica del momento coniugato, allora se prendiamo:
) che ci aveva permesso di scrivere
l'equazione di Dirac per la particella libera, però questa varrà ancora per la
parte cinetica del momento coniugato, allora se prendiamo:
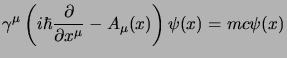
![]() è un quadrivettore, si dimostra con l'esatto identico procedimento
dello scorso capitolo, dato che
è un quadrivettore, si dimostra con l'esatto identico procedimento
dello scorso capitolo, dato che ![]() trasforma esattamente come
trasforma esattamente come
![]() per cui in quanto visto al §2.3.2 basta sostituire a
quest'ultimo
per cui in quanto visto al §2.3.2 basta sostituire a
quest'ultimo
![]() .
.

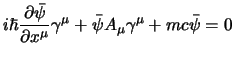
![]() e la
(2.114) a sinistra per
e la
(2.114) a sinistra per ![]() e si sommano, in questo modo i
termini nel potenziale e in
e si sommano, in questo modo i
termini nel potenziale e in ![]() se ne vanno e resta solo:
se ne vanno e resta solo:
![]() è sempre definito a meno di una
trasformazione di gauge, per cui se prendiamo un altro potenziale:
è sempre definito a meno di una
trasformazione di gauge, per cui se prendiamo un altro potenziale: