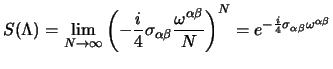Next: Proprietà delle trasformazioni degli
Up: Covarianza dell'equazione di Dirac
Previous: Le proprietà delle matrici
Contents
Index
La prova della covarianza
Se vogliamo dimostrare che l'equazione di Dirac è covariante basterà mostrare
che se 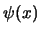 è lo spinore che descrive una particella in un certo sistema
inerziale, in un qualsiasi altro sistema inerziale possiamo trovare, con
un'opportuna legge di trasformazione, uno spinore
è lo spinore che descrive una particella in un certo sistema
inerziale, in un qualsiasi altro sistema inerziale possiamo trovare, con
un'opportuna legge di trasformazione, uno spinore 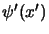 che dia gli
stessi risultati fisici di
che dia gli
stessi risultati fisici di 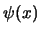 .
.
Questo allora comporta che anche 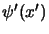 dovrà essere soluzione
dell'equazione di Dirac (2.18); in generale dunque dovrà essere:
dovrà essere soluzione
dell'equazione di Dirac (2.18); in generale dunque dovrà essere:
dove le
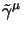 non è detto siano esattamente le stesse viste
in §2.3.1, in quanto l'unica condizione che possiamo imporre è
che anch'esse soddisfino le relazioni (2.22) e
(2.21); ma abbiamo detto che comunque tutte le
non è detto siano esattamente le stesse viste
in §2.3.1, in quanto l'unica condizione che possiamo imporre è
che anch'esse soddisfino le relazioni (2.22) e
(2.21); ma abbiamo detto che comunque tutte le
 sono equivalenti a meno di una trasformazione unitaria, per cui
si può tranquillamente richiedere che sia:
sono equivalenti a meno di una trasformazione unitaria, per cui
si può tranquillamente richiedere che sia:
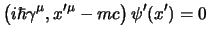 |
(3.23) |
e se riusciamo a trovare la trasformazione degli spinori che ci permette di
verificare questa, la covarianza è dimostrata.
Il primo caso, molto semplice, è quello delle traslazioni; in tal caso la
trasformazione si può scrivere nella forma più generale come:
dove  è un qualunque vettore costante; in questo caso basta prendere:
e dato che ovviamente:
la (2.23) è immediatamente soddisfatta.
Dunque per quanto riguarda le traslazioni la covarianza è dimostrata.
è un qualunque vettore costante; in questo caso basta prendere:
e dato che ovviamente:
la (2.23) è immediatamente soddisfatta.
Dunque per quanto riguarda le traslazioni la covarianza è dimostrata.
Resta da vedere cosa succede nel caso una trasformazione di Lorentz generica
(comprendente sia boost che rotazioni spaziali) da un sistema 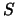 ad un
sistema
ad un
sistema 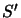 . Abbiamo visto in §1.1.2 la legge di
trasformazione delle coordinate (1.19) e le sue
proprietà: che conserva l'elemento di linea
. Abbiamo visto in §1.1.2 la legge di
trasformazione delle coordinate (1.19) e le sue
proprietà: che conserva l'elemento di linea 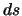 , quali sono le condizioni su
, quali sono le condizioni su
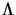 e che per trasformazioni proprie
e che per trasformazioni proprie
 .
.
Essendo sia le trasformazioni di Lorentz che l'equazione di Dirac lineari
cercheremo anche la trasformazione dello spinore nella forma di una
trasformazione lineare (ovviamente non singolare)
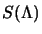 tale che:
tale che:
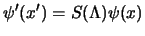 |
(3.24) |
che dipenda solo dai parametri della trasformazione di Lorentz. Da questa con
la (1.19) si ottiene:
e viceversa si avrà che:
d'altra parte siccome 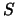 e
e 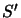 sono completamente arbitrari possiamo
applicare la (2.24) nel passaggio inverso da
sono completamente arbitrari possiamo
applicare la (2.24) nel passaggio inverso da 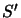 a
a
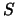 ottenendo:
che confrontata con la precedente ci permette di scrivere:
allo stesso modo si può dimostrare che se
ottenendo:
che confrontata con la precedente ci permette di scrivere:
allo stesso modo si può dimostrare che se  e
e  sono due
trasformazioni di Lorentz si ha:
che unita alla precedente ci dice che le
sono due
trasformazioni di Lorentz si ha:
che unita alla precedente ci dice che le
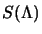 formano un gruppo
continuo (l'unità è
formano un gruppo
continuo (l'unità è
 ) rispetto ai parametri delle
trasformazioni di Lorentz.
) rispetto ai parametri delle
trasformazioni di Lorentz.
Vediamo adesso cosa comporta la condizione che 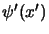 continui a
soddisfare la (2.23); dalla
(2.18) per
continui a
soddisfare la (2.23); dalla
(2.18) per 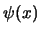 si ha che:
si ha che:
da questa, considerando che
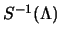 non dipende dalle coordinate, si
ha:
che moltiplicata a sinistra per
non dipende dalle coordinate, si
ha:
che moltiplicata a sinistra per
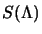 diventa:
e vogliamo che questa si riduca alla
(2.23); ma dalla trasformazione delle
coordinate si ottiene subito che:
dunque sostituendo si ha:
e perché questa dia la (2.23) dovrà essere:
e questa è la condizione che devono soddisfare le
diventa:
e vogliamo che questa si riduca alla
(2.23); ma dalla trasformazione delle
coordinate si ottiene subito che:
dunque sostituendo si ha:
e perché questa dia la (2.23) dovrà essere:
e questa è la condizione che devono soddisfare le
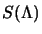 , un altro modo
di scriverla si ottiene moltiplicandola a sinistra per
, un altro modo
di scriverla si ottiene moltiplicandola a sinistra per
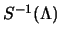 e a
destra per
e a
destra per
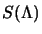 :
:
 |
(3.25) |
che ci da la legge di trasformazione delle
 . Sappiamo poi che le
trasformazioni devono conservare la metrica, e nel
§1.1.2 abbiamo visto come questo si traduce nella
condizione sulle
. Sappiamo poi che le
trasformazioni devono conservare la metrica, e nel
§1.1.2 abbiamo visto come questo si traduce nella
condizione sulle
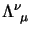 espressa in
(1.21), un altro modo di scrivere quella relazione è:
espressa in
(1.21), un altro modo di scrivere quella relazione è:
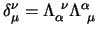 |
(3.26) |
(con un po' di conti la si trova facilmente da
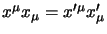 ) e
si può riscrivere la (2.25) nella forma:
) e
si può riscrivere la (2.25) nella forma:
 |
(3.27) |
Abbiamo visto prima che le
 costituiscono un gruppo continuo nei
parametri della trasformazione di Lorentz; l'ipotesi che si fa, e che
verificheremo essere corretta trovandolo, è che questo sia un gruppo di Lie,
per cui potremo, sfruttando la (2.27) e la
(2.26), cominciare a costruire
costituiscono un gruppo continuo nei
parametri della trasformazione di Lorentz; l'ipotesi che si fa, e che
verificheremo essere corretta trovandolo, è che questo sia un gruppo di Lie,
per cui potremo, sfruttando la (2.27) e la
(2.26), cominciare a costruire
 partendo dalle trasformazioni infinitesime:
partendo dalle trasformazioni infinitesime:
 |
(3.28) |
per la (2.26) si avrà che:
adesso in questa l'ultimo termine è del secondo ordine e si può trascurare,
mentre per il primo si ha banalmente
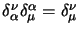 quindi si annulla col primo membro e alla fine resta, cambiati
gli indici con le restanti
quindi si annulla col primo membro e alla fine resta, cambiati
gli indici con le restanti 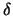 :
da cui, passando ad indici controvarianti:
vale a dire che i parametri infinitesimi della trasformazione sono
antisimmetrici, da cui segue che solo sei sono indipendenti, e riotteniamo
quanto già accennato al §1.1.2. I coefficienti
:
da cui, passando ad indici controvarianti:
vale a dire che i parametri infinitesimi della trasformazione sono
antisimmetrici, da cui segue che solo sei sono indipendenti, e riotteniamo
quanto già accennato al §1.1.2. I coefficienti
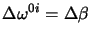 provocano un boost di Lorentz infinitesimale
di velocità
provocano un boost di Lorentz infinitesimale
di velocità
 nella direzione
nella direzione 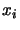 , mentre i
, mentre i
 generano una rotazione spaziale
infinitesimale di angolo
generano una rotazione spaziale
infinitesimale di angolo
 intorno all'asse
intorno all'asse 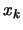 con
con
 .
.
Adesso per ottenere
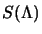 utilizziamo l'ipotesi che sia un gruppo di
Lie per cui esiste uno sviluppo in serie rispetto ai parametri che,
arrestandoci al primo ordine; scriveremo come:
utilizziamo l'ipotesi che sia un gruppo di
Lie per cui esiste uno sviluppo in serie rispetto ai parametri che,
arrestandoci al primo ordine; scriveremo come:
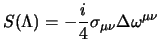 |
(3.29) |
(si è esplicitato il fattore 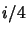 per motivi di comodità) dove
per motivi di comodità) dove
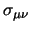 , detti anche generatori del gruppo, sono matrici
, detti anche generatori del gruppo, sono matrici
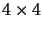 ; da questa, essendo la
; da questa, essendo la 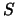 nella forma infinitesima
nella forma infinitesima
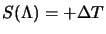 si ottiene immediatamente che:
si ottiene immediatamente che:
 |
(3.30) |
(è banale osservare che in tal caso, fermandoci al primo ordine, è
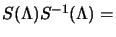 ) inoltre si noti che siccome abbiamo solo sei
parametri indipendenti anche le
) inoltre si noti che siccome abbiamo solo sei
parametri indipendenti anche le
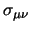 , dovranno essere
antisimmetriche negli indici per essere indipendenti (d'altronde nella
sommatoria una eventuale parte simmetrica verrebbe automaticamente cancellata
essendo antisimmetrici i
, dovranno essere
antisimmetriche negli indici per essere indipendenti (d'altronde nella
sommatoria una eventuale parte simmetrica verrebbe automaticamente cancellata
essendo antisimmetrici i
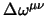 ); dunque sarà:
cosicché ai sei parametri delle trasformazioni di Lorentz corrispondono questi
sei generatori.
); dunque sarà:
cosicché ai sei parametri delle trasformazioni di Lorentz corrispondono questi
sei generatori.
Una ulteriore condizione sulle
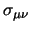 si può ottenere normalizzando
la trasformazione; se infatti si moltiplica
si può ottenere normalizzando
la trasformazione; se infatti si moltiplica
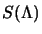 per un qualunque
numero complesso tutte le relazioni precedenti sono ancora soddisfatte e si
riottiene comunque l'equazione di Dirac; si può eliminare parte di questa
ambiguità richiedendo che il determinante sia unitario (resta sempre la
possibilità di moltiplicare per radici quartiche di uno), nel nostro caso,
avendo una matrice infinitesima, vale la relazione:
per un qualunque
numero complesso tutte le relazioni precedenti sono ancora soddisfatte e si
riottiene comunque l'equazione di Dirac; si può eliminare parte di questa
ambiguità richiedendo che il determinante sia unitario (resta sempre la
possibilità di moltiplicare per radici quartiche di uno), nel nostro caso,
avendo una matrice infinitesima, vale la relazione:
quindi nel nostro caso la condizione
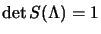 si traduce in:
e dunque, dato che i coefficienti sono tutti indipendenti (evidentemente pure
si traduce in:
e dunque, dato che i coefficienti sono tutti indipendenti (evidentemente pure
 è antisimmetrico) si ha che:
è antisimmetrico) si ha che:
Adesso possiamo usare le espressioni (2.28),
(2.29) e
(2.30) delle varie trasfromazioni
infinitesime nella (2.25) per ottenere una equazione
per le
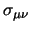 ; sostituendo si avrà che:
; sostituendo si avrà che:
da questa, scartati tutti i termini del secondo ordine in
 ,
si ha:
che, semplificato il primo termine e raccolto a secondo membro, diventa:
,
si ha:
che, semplificato il primo termine e raccolto a secondo membro, diventa:
![$\displaystyle \Delta\omega^\nu_{\ \mu}\gamma^\mu = - { i\over 4}\Delta\omega^{\alpha\beta} [\gamma^\nu,\sigma_{\alpha\beta}]$](img678.png) |
(3.31) |
adesso in questa dobbiamo fattorizzare i parametri
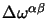 , per questo possiamo scriverci:
ma in questa espressione i fattori non sono tutti indipendenti, dato che
, per questo possiamo scriverci:
ma in questa espressione i fattori non sono tutti indipendenti, dato che
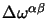 è antisimmetrico mentre
è antisimmetrico mentre
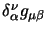 no, allora se vogliamo una fattorizzazione in termini di
coefficienti indipendenti occorre eliminarne la parte simmetrica (che nella
sommatoria è identicamente nulla) e riscriverla antisimmetrizzando come:
adesso questa si può sostituire nella
(2.31), ottenendo:
in questa tutti i fattori dei
no, allora se vogliamo una fattorizzazione in termini di
coefficienti indipendenti occorre eliminarne la parte simmetrica (che nella
sommatoria è identicamente nulla) e riscriverla antisimmetrizzando come:
adesso questa si può sostituire nella
(2.31), ottenendo:
in questa tutti i fattori dei
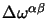 sono
antisimmetrici e dato che questi ultimi sono arbitrari ed indipendenti si
possono tranquillamente semplificare ottenendo:
e se portiamo gli indici
sono
antisimmetrici e dato che questi ultimi sono arbitrari ed indipendenti si
possono tranquillamente semplificare ottenendo:
e se portiamo gli indici
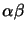 in alto e svolgiamo i conti si
ha la definitiva:
in alto e svolgiamo i conti si
ha la definitiva:
![$\displaystyle [\gamma^\nu,\sigma^{\alpha\beta}]= 2 i (g^{\nu\alpha} \gamma^\beta -g^{\nu\beta} \gamma^\alpha )$](img686.png) |
(3.32) |
che è l'espressione finale.
Si tratta allora di trovare sei matrici
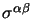 che soddisfino
questa condizione; il tentativo più semplice è allora cercare le
che soddisfino
questa condizione; il tentativo più semplice è allora cercare le
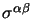 nella forma di un prodotto antisimmetrico delle
nella forma di un prodotto antisimmetrico delle
 , e si può verificare con le relazioni di anticommutazione che se
si prende:
, e si può verificare con le relazioni di anticommutazione che se
si prende:
![$\displaystyle \sigma^{\alpha\beta}={i \over 2} [\gamma^\alpha,\gamma^\beta]$](img688.png) |
(3.33) |
queste effettivamente soddisfano la (2.32) e le
altre condizioni richieste.
Una volta che il problema è stato risolto per trasformazioni infinitesime esso
si può risolvere in generale con un procedimento di iterazione, infatti nel
caso di un valore finito dei parametri
 basterà dividere il
valore in
basterà dividere il
valore in 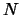 parti e iterare la formula facendo poi tendere
parti e iterare la formula facendo poi tendere 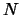 all'infinito;
allora se
all'infinito;
allora se
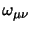 sono i valori dei parametri della trasformazione
(sono detti angoli covarianti per analogia con gli angoli di Eulero delle
rotazioni tridimensionali) si può dimostrare che la trasformazione degli
spinori assume la forma generale:
sono i valori dei parametri della trasformazione
(sono detti angoli covarianti per analogia con gli angoli di Eulero delle
rotazioni tridimensionali) si può dimostrare che la trasformazione degli
spinori assume la forma generale:
che si può riscrivere, sommando solo su fattori indipendenti (cioè con
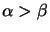 ) come:
) come:
 |
(3.34) |
e si noti che come per le rotazioni degli spinori classici compare il fattore
 che fa si che dopo una rotazione spaziale di
che fa si che dopo una rotazione spaziale di 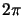 lo spinore cambi
segno (non è quindi un normale vettore) per ritornare lo stesso solo dopo
lo spinore cambi
segno (non è quindi un normale vettore) per ritornare lo stesso solo dopo
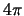 . Questa ambiguità non ha comunque nessuna conseguenza perché tutte le
quantità fisiche osservabili devono essere bilineari negli spinori.
. Questa ambiguità non ha comunque nessuna conseguenza perché tutte le
quantità fisiche osservabili devono essere bilineari negli spinori.
Con questo abbiamo dimostrato la covarianza dell'equazione di Dirac e trovato
la matrice di trasformazione degli spinori, anche se limitatamente alle
trasformazioni proprie, dato che il procedimento di iterazione porta solo alle
trasformazioni connesse con l'identità.





Next: Proprietà delle trasformazioni degli
Up: Covarianza dell'equazione di Dirac
Previous: Le proprietà delle matrici
Contents
Index
Simone Piccardi
2003-02-20
![]() è lo spinore che descrive una particella in un certo sistema
inerziale, in un qualsiasi altro sistema inerziale possiamo trovare, con
un'opportuna legge di trasformazione, uno spinore
è lo spinore che descrive una particella in un certo sistema
inerziale, in un qualsiasi altro sistema inerziale possiamo trovare, con
un'opportuna legge di trasformazione, uno spinore ![]() che dia gli
stessi risultati fisici di
che dia gli
stessi risultati fisici di ![]() .
.
![]() dovrà essere soluzione
dell'equazione di Dirac (2.18); in generale dunque dovrà essere:
dovrà essere soluzione
dell'equazione di Dirac (2.18); in generale dunque dovrà essere:
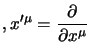
![]() ad un
sistema
ad un
sistema ![]() . Abbiamo visto in §1.1.2 la legge di
trasformazione delle coordinate (1.19) e le sue
proprietà: che conserva l'elemento di linea
. Abbiamo visto in §1.1.2 la legge di
trasformazione delle coordinate (1.19) e le sue
proprietà: che conserva l'elemento di linea ![]() , quali sono le condizioni su
, quali sono le condizioni su
![]() e che per trasformazioni proprie
e che per trasformazioni proprie
![]() .
.
![]() tale che:
tale che:
![]() continui a
soddisfare la (2.23); dalla
(2.18) per
continui a
soddisfare la (2.23); dalla
(2.18) per ![]() si ha che:
si ha che:
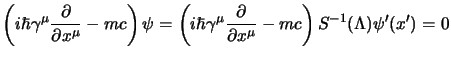
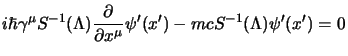
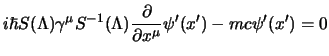
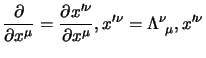
![]() costituiscono un gruppo continuo nei
parametri della trasformazione di Lorentz; l'ipotesi che si fa, e che
verificheremo essere corretta trovandolo, è che questo sia un gruppo di Lie,
per cui potremo, sfruttando la (2.27) e la
(2.26), cominciare a costruire
costituiscono un gruppo continuo nei
parametri della trasformazione di Lorentz; l'ipotesi che si fa, e che
verificheremo essere corretta trovandolo, è che questo sia un gruppo di Lie,
per cui potremo, sfruttando la (2.27) e la
(2.26), cominciare a costruire
![]() partendo dalle trasformazioni infinitesime:
partendo dalle trasformazioni infinitesime:
![]() utilizziamo l'ipotesi che sia un gruppo di
Lie per cui esiste uno sviluppo in serie rispetto ai parametri che,
arrestandoci al primo ordine; scriveremo come:
utilizziamo l'ipotesi che sia un gruppo di
Lie per cui esiste uno sviluppo in serie rispetto ai parametri che,
arrestandoci al primo ordine; scriveremo come:
![]() si può ottenere normalizzando
la trasformazione; se infatti si moltiplica
si può ottenere normalizzando
la trasformazione; se infatti si moltiplica
![]() per un qualunque
numero complesso tutte le relazioni precedenti sono ancora soddisfatte e si
riottiene comunque l'equazione di Dirac; si può eliminare parte di questa
ambiguità richiedendo che il determinante sia unitario (resta sempre la
possibilità di moltiplicare per radici quartiche di uno), nel nostro caso,
avendo una matrice infinitesima, vale la relazione:
per un qualunque
numero complesso tutte le relazioni precedenti sono ancora soddisfatte e si
riottiene comunque l'equazione di Dirac; si può eliminare parte di questa
ambiguità richiedendo che il determinante sia unitario (resta sempre la
possibilità di moltiplicare per radici quartiche di uno), nel nostro caso,
avendo una matrice infinitesima, vale la relazione:
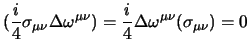
![]() ; sostituendo si avrà che:
; sostituendo si avrà che:
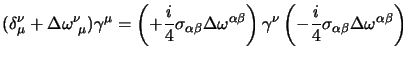
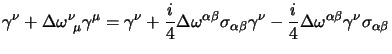
![$\displaystyle \half
(g^\nu_\alpha g_{\mu\beta}-g^\nu_\beta g_{\mu\alpha})
\Del...
...\mu =
-{i\over 4}\Delta\omega^{\alpha\beta} [\gamma^\nu,\sigma_{\alpha\beta}]
$](img683.png)
![]() che soddisfino
questa condizione; il tentativo più semplice è allora cercare le
che soddisfino
questa condizione; il tentativo più semplice è allora cercare le
![]() nella forma di un prodotto antisimmetrico delle
nella forma di un prodotto antisimmetrico delle
![]() , e si può verificare con le relazioni di anticommutazione che se
si prende:
, e si può verificare con le relazioni di anticommutazione che se
si prende:
![]() basterà dividere il
valore in
basterà dividere il
valore in ![]() parti e iterare la formula facendo poi tendere
parti e iterare la formula facendo poi tendere ![]() all'infinito;
allora se
all'infinito;
allora se
![]() sono i valori dei parametri della trasformazione
(sono detti angoli covarianti per analogia con gli angoli di Eulero delle
rotazioni tridimensionali) si può dimostrare che la trasformazione degli
spinori assume la forma generale:
sono i valori dei parametri della trasformazione
(sono detti angoli covarianti per analogia con gli angoli di Eulero delle
rotazioni tridimensionali) si può dimostrare che la trasformazione degli
spinori assume la forma generale: