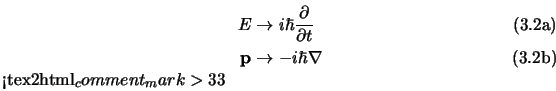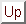



Next: L'equazione di Klein-Gordon
Up: Lo scontro fra meccanica
Previous: Alcuni concetti base
Contents
Index
La costruzione di un'equazione relativistica
Per tentare di costruire un'equazione che combini invarianza relativistica e
meccanica quantistica osserviamo che dal principio di corrispondenza e
dall'equazione di Schroedinger si possono derivare le due relazioni:
e notiamo che queste si possono agevolmente riassumere in forma covariante
come:
 |
(3.4) |
Nella meccanica quantistica classica l'equazione per una particella singola
libera si ottiene partendo dalla espressione classica dell'energia:
sostituendo in questa gli operatori delle
(2.3); in relatività però l'equazione che da
l'energia è:
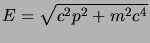 |
(3.5) |
e questa non la si può quantizzare così banalmente, perché nasce il problema
dell'operatore radice quadrata. Esso infatti può essere definito solo come
serie di potenze, e questo, comportando derivate spaziali di ogni ordine, da
luogo ad un'equazione non locale, assolutamente intrattabile. Inoltre usando
questa espressione si perderebbe completamente la simmetria fra tempo e spazio
tipica della relatività.




Next: L'equazione di Klein-Gordon
Up: Lo scontro fra meccanica
Previous: Alcuni concetti base
Contents
Index
Simone Piccardi
2003-02-20