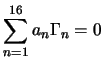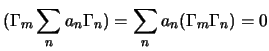Next: Gli operatori di traslazione
Up: Covarianza dell'equazione di Dirac
Previous: Le trasformazioni improprie
Contents
Index
I covarianti di Dirac
In generale le matrici  possono essere espresse tramite una base di
16 matrici indipendenti; evidentemente le
possono essere espresse tramite una base di
16 matrici indipendenti; evidentemente le
 non coprono tutto lo
spazio delle matrici
non coprono tutto lo
spazio delle matrici  , e si può dimostrare che non lo fa neanche
l'algebra da esse derivata, ma si possono comunque costruire con le
, e si può dimostrare che non lo fa neanche
l'algebra da esse derivata, ma si possono comunque costruire con le
 16 matrici indipendenti che risultano molto utili nelle
applicazioni di calcolo e hanno proprietà di trasformazione ben definite.
16 matrici indipendenti che risultano molto utili nelle
applicazioni di calcolo e hanno proprietà di trasformazione ben definite.
La prima matrice che ci interessa è stata indicata, con una notazione un po'
strana che resta in uso per motivi storici, come 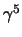 ; essa è definita
da:
; essa è definita
da:
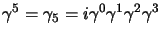 |
(3.48) |
(l'indice non è covariante e non ha importanza dove lo si mette) se usiamo la
rappresentazione di Dirac basta fare i conti per ottenere che:
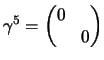 |
(3.49) |
una definizione equivalente che usa il tensore di Ricci (e ci fa capire meglio
le proprietà di trasformazione) è:
 |
(3.50) |
l'equivalenza con la precedente definizione si verifica immediatamente,
infatti se due indici qualsiasi delle 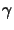 sono uguali il termine è nullo
per via del tensore di Ricci, e nella somma restano solo i 4! termini con gli
indici tutti diversi; ciascuno di essi però sarà una permutazione pari o
dispari della sequenza fondamentale
sono uguali il termine è nullo
per via del tensore di Ricci, e nella somma restano solo i 4! termini con gli
indici tutti diversi; ciascuno di essi però sarà una permutazione pari o
dispari della sequenza fondamentale
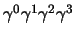 e ci si
potrà riportare a questa con un numero pari o dispari di scambi grazie alle
relazioni di anticommutazione, ma il segno meno che viene fuori per le
permutazioni dispari viene annullato dall'analogo segno del tensore di Ricci,
per cui alla fine tutti questi termini sono uguali, ed avendo diviso per 4! si
riottiene la (2.48).
e ci si
potrà riportare a questa con un numero pari o dispari di scambi grazie alle
relazioni di anticommutazione, ma il segno meno che viene fuori per le
permutazioni dispari viene annullato dall'analogo segno del tensore di Ricci,
per cui alla fine tutti questi termini sono uguali, ed avendo diviso per 4! si
riottiene la (2.48).
Dalla definizione si ottengono le proprietà di 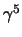 , è abbastanza facile
verificare ad esempio, sempre attraverso le regole di anticommutazione, che:
, è abbastanza facile
verificare ad esempio, sempre attraverso le regole di anticommutazione, che:
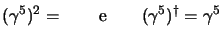 |
(3.51) |
(per la seconda occorre anche la (2.21)), si tratta solo
di fare un po' di conti usando l'espressione (2.48),
stando attenti ai segni. Un'altra relazione è che:
 |
(3.52) |
se lo scriviamo esplicitamente come
 si nota che, essendo una a
destra e l'altra a sinistra, per portare
si nota che, essendo una a
destra e l'altra a sinistra, per portare
 a fianco della sua
corrispettiva in ciascun addendo ci vorrà un numero di scambi pari per uno e
dispari per l'altro o viceversa, per cui emerge una differenza di segno che
cancella gli addendi divenuti uguali e dimostra la
(2.52).
a fianco della sua
corrispettiva in ciascun addendo ci vorrà un numero di scambi pari per uno e
dispari per l'altro o viceversa, per cui emerge una differenza di segno che
cancella gli addendi divenuti uguali e dimostra la
(2.52).
Una volta definita 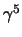 si possono infine definire una serie di matrici
indipendenti che possano essere usata come base per lo spazio delle matrici
si possono infine definire una serie di matrici
indipendenti che possano essere usata come base per lo spazio delle matrici
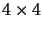 , queste matrici sono dette covarianti di Dirac, e la lro
definizione è:
, queste matrici sono dette covarianti di Dirac, e la lro
definizione è:
 |
(3.53) |
Vediamo allora perché queste matrici, che indicheremo genericamente con
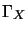 , sono dette covarianti di Dirac; sappiamo infatti che si può
parlare di covarianza solo per enti come scalari, vettori, tensori le cui
componenti sono quantità numeriche ma non matrici; vedremo che in realtà
quello che ha le proprietà di trasformazione riportate nella tabella in
(2.53) non è tanto la singola
, sono dette covarianti di Dirac; sappiamo infatti che si può
parlare di covarianza solo per enti come scalari, vettori, tensori le cui
componenti sono quantità numeriche ma non matrici; vedremo che in realtà
quello che ha le proprietà di trasformazione riportate nella tabella in
(2.53) non è tanto la singola 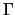 quanto
le forme bilineari negli spinori
quanto
le forme bilineari negli spinori
 che si possono
costruire a partire da esse.
che si possono
costruire a partire da esse.
Si tratterà allora di studiare le proprietà di trasformazione di queste forme
bilineari verificando che esse corrispondano a quelle riportate nella
(2.53); al §2.3.4 abbiamo
trovato le proprietà di trasformazione degli spinori che sono:
allora è immediato verificare il carattere scalare di 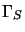 dato che:
mentre il carattere vettoriale di
dato che:
mentre il carattere vettoriale di
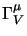 lo abbiamo già visto al
§2.3.4 per la quadricorrente; il procedimento per
lo abbiamo già visto al
§2.3.4 per la quadricorrente; il procedimento per
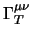 è lo stesso solo con un po' più di conti:
in questa poi si può inserire il prodotto
è lo stesso solo con un po' più di conti:
in questa poi si può inserire il prodotto 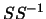 fra la
fra la 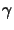 ottenendo:
ed usare per ciascun
ottenendo:
ed usare per ciascun
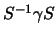 la (2.25)
ottenendo:
ma dato che le somme sui diversi addendi sono indipendenti e gli indici
ripetuti sono qualunque questa si può raccogliere
la (2.25)
ottenendo:
ma dato che le somme sui diversi addendi sono indipendenti e gli indici
ripetuti sono qualunque questa si può raccogliere
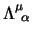 e
e
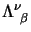 ponendo
ponendo
 e
e
 , per cui si
ha:
che è quanto si voleva dimostrare.
, per cui si
ha:
che è quanto si voleva dimostrare.
Restano da esaminare le ultime due, per farlo però bisogna chiarire cosa
significano pseudoscalare e pseudovettoriale, per questo basta ricordare
quanto visto al §1.1.2 quando si sono definite le
densità tensoriali: uno pseudoscalare è una quantità che trasforma come
l'elemento di volume, cioè una densità scalare di peso 1, mentre uno
pseudovettore è una densità vettoriale, sempre di peso 1, sono cioè due
quantità che oltre alla normale trasformazione acquisiscono a fattore lo
jacobiano
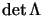 .
.
Vediamo allora cosa succede con 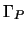 ; partiamo dalla definizione in
(2.53) usando per
; partiamo dalla definizione in
(2.53) usando per 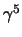 l'espressione
(2.50); allora si avrà:
l'espressione
(2.50); allora si avrà:
adesso si inseriscono le solite  fra le
fra le 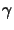 e sempre usando
la (2.25) si ottiene:
e adesso possiamo usare per la parte in parentesi quadra la proprietà
fondamentale del tensore di Ricci (1.28) vista
al §1.1.2, ottenendo alla fine:
e quindi questo è uno pseudoscalare. Vista questa è immediato ottenere
l'analoga anche per
e sempre usando
la (2.25) si ottiene:
e adesso possiamo usare per la parte in parentesi quadra la proprietà
fondamentale del tensore di Ricci (1.28) vista
al §1.1.2, ottenendo alla fine:
e quindi questo è uno pseudoscalare. Vista questa è immediato ottenere
l'analoga anche per
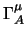 dato che:
e adesso per ciascun pezzo possiamo usare quanto già ottenuto per cui alla
fine:
riassumendo si ha che:
dato che:
e adesso per ciascun pezzo possiamo usare quanto già ottenuto per cui alla
fine:
riassumendo si ha che:
Le 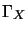 godono di una serie di proprietà importanti che però non staremo
a dimostrare per intero; è però importante notare che a parte la presenza di
un fattore
godono di una serie di proprietà importanti che però non staremo
a dimostrare per intero; è però importante notare che a parte la presenza di
un fattore  immaginario in alcune di esse possono essere raggruppate in
maniera naturale secondo la seguente tabella (vedi [Mes]):
immaginario in alcune di esse possono essere raggruppate in
maniera naturale secondo la seguente tabella (vedi [Mes]):
Table 2.1:
Tabella delle matrici di Dirac
| Matrice |
Forma esplicita |
| di Dirac |
 |
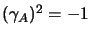 (S)
(S) |
|
dove con la notazione
![$ \gamma^{[\mu\nu\ldots]}$](img834.png) intenderemo il prodotto di
una, due, tre o quattro
intenderemo il prodotto di
una, due, tre o quattro
 con indici diversi; è banale osservare
che queste altro non sono che le componenti delle
con indici diversi; è banale osservare
che queste altro non sono che le componenti delle 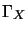 di
(2.54); ma usando questa tabella è molto
più facile ottenere le proprietà generale delle
di
(2.54); ma usando questa tabella è molto
più facile ottenere le proprietà generale delle 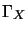 che sono:
che sono:

La proprietà 1) la abbiamo già vista per 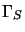 ,
, 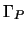 e
e  ;
in ogni caso guardando alle singoli componenti di 2.1 si
vede subito che qualunque sia il quadrato scelto si avranno sempre due matrici
uguali per ciascun indice diverso, che con un opportuno numero di
anticommutazioni (da cui il segno) potranno essere poste a fianco e quindi
semplificate fino ad arrivare
;
in ogni caso guardando alle singoli componenti di 2.1 si
vede subito che qualunque sia il quadrato scelto si avranno sempre due matrici
uguali per ciascun indice diverso, che con un opportuno numero di
anticommutazioni (da cui il segno) potranno essere poste a fianco e quindi
semplificate fino ad arrivare 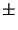 .
.
La proprietà 2) la abbiamo già vista per le  e
e 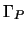 , per le
altre basta notare che per le
, per le
altre basta notare che per le
![$ \gamma^{[\mu\nu\rho]}$](img838.png) si può scegliere la
opportuna
si può scegliere la
opportuna
 in modo da avere un prodotto con quattro indici diversi,
ed idem fra le
in modo da avere un prodotto con quattro indici diversi,
ed idem fra le
![$ \gamma^{[\mu\nu]}$](img839.png) e poi facendo le opportune anticommutazioni
si ha la proprietà.
e poi facendo le opportune anticommutazioni
si ha la proprietà.
La proprietà 3) si ricava dalle due precedenti; infatti data 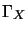 sia
sia
 quella che anticommuta, allora si avrà che:
quella che anticommuta, allora si avrà che:
dove il primo passaggio è per la proprietà 1) il secondo per la proprietà
ciclica della traccia il terzo per la proprietà 2) ed il quarto tornando
indietro con la 1).
La proprietà 4) si capisce subito notando che qualunque sia il prodotto con un
opportuno numero di anticommutazioni si può sempre eliminare le eventuali
 doppie ritornando, eventualmente con un segno opposto, ad
un'altra delle matrici di tab. 2.1 facendo i conti
effettivi si vede anche che con la scelta di
(2.54) il segno è sempre positivo.
doppie ritornando, eventualmente con un segno opposto, ad
un'altra delle matrici di tab. 2.1 facendo i conti
effettivi si vede anche che con la scelta di
(2.54) il segno è sempre positivo.
La proprietà 5) invece si dimostra con le precedenti; consideriamo che sia:
e moltiplichiamo questa per una qualunque 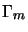 prendendo poi la traccia;
per la linearità si ottiene che:
ma per la proprietà 4) se
prendendo poi la traccia;
per la linearità si ottiene che:
ma per la proprietà 4) se 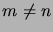 il prodotto
il prodotto
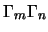 ci da una
ci da una
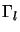 la cui traccia, per la proprietà 3) è nulla; allora nella traccia
resta solo il termine in
la cui traccia, per la proprietà 3) è nulla; allora nella traccia
resta solo il termine in
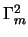 la cui traccia per la 1) è
la cui traccia per la 1) è  dunque deve essere
dunque deve essere 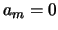 , questo vale per tutti gli
, questo vale per tutti gli 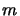 dunque si è
dimostrato che le
dunque si è
dimostrato che le 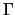 sono linearmente indipendenti.
sono linearmente indipendenti.
Ci sono poi ulteriori relazioni interessanti concernenti queste matrici, la
prima è:
 |
(3.55) |
che è importante e ci servirà in seguito, la dimostrazione è piuttosto facile
anche se noiosa, perché basta verificarla per componenti, scrivendosi tutto in
termini delle
 ed usando le proprietà delle
ed usando le proprietà delle
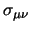 e del
tensore di Ricci; la seconda relazione invece è:
e del
tensore di Ricci; la seconda relazione invece è:
![$\displaystyle [\gamma^5,\sigma^{\mu\nu}]=0$](img853.png) |
(3.56) |
dalla proprietà di anticommutazione con le
 segue infatti che:
dunque
segue infatti che:
dunque
![$ [\gamma^5,\gamma^\nu\gamma^\mu]=0$](img855.png) per cui vale anche la (2.56); da essa segue poi
che per trasformazioni di Lorentz proprie vale anche:
in quanto
per cui vale anche la (2.56); da essa segue poi
che per trasformazioni di Lorentz proprie vale anche:
in quanto
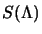 è funzione delle
è funzione delle
 ; nel caso della
parità dall'espressione ottenuta al paragrafo precedente si ha invece che:
infine possiamo avere le espressioni per i coniugati hermitiani di
; nel caso della
parità dall'espressione ottenuta al paragrafo precedente si ha invece che:
infine possiamo avere le espressioni per i coniugati hermitiani di
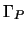 e
e
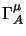 che, con le solite regole di commutazione e la
(2.21) sono:
che, con le solite regole di commutazione e la
(2.21) sono:





Next: Gli operatori di traslazione
Up: Covarianza dell'equazione di Dirac
Previous: Le trasformazioni improprie
Contents
Index
Simone Piccardi
2003-02-20
![]() possono essere espresse tramite una base di
16 matrici indipendenti; evidentemente le
possono essere espresse tramite una base di
16 matrici indipendenti; evidentemente le
![]() non coprono tutto lo
spazio delle matrici
non coprono tutto lo
spazio delle matrici ![]() , e si può dimostrare che non lo fa neanche
l'algebra da esse derivata, ma si possono comunque costruire con le
, e si può dimostrare che non lo fa neanche
l'algebra da esse derivata, ma si possono comunque costruire con le
![]() 16 matrici indipendenti che risultano molto utili nelle
applicazioni di calcolo e hanno proprietà di trasformazione ben definite.
16 matrici indipendenti che risultano molto utili nelle
applicazioni di calcolo e hanno proprietà di trasformazione ben definite.
![]() ; essa è definita
da:
; essa è definita
da:
![]() , è abbastanza facile
verificare ad esempio, sempre attraverso le regole di anticommutazione, che:
, è abbastanza facile
verificare ad esempio, sempre attraverso le regole di anticommutazione, che:
![]() si possono infine definire una serie di matrici
indipendenti che possano essere usata come base per lo spazio delle matrici
si possono infine definire una serie di matrici
indipendenti che possano essere usata come base per lo spazio delle matrici
![]() , queste matrici sono dette covarianti di Dirac, e la lro
definizione è:
, queste matrici sono dette covarianti di Dirac, e la lro
definizione è:
![]() , sono dette covarianti di Dirac; sappiamo infatti che si può
parlare di covarianza solo per enti come scalari, vettori, tensori le cui
componenti sono quantità numeriche ma non matrici; vedremo che in realtà
quello che ha le proprietà di trasformazione riportate nella tabella in
(2.53) non è tanto la singola
, sono dette covarianti di Dirac; sappiamo infatti che si può
parlare di covarianza solo per enti come scalari, vettori, tensori le cui
componenti sono quantità numeriche ma non matrici; vedremo che in realtà
quello che ha le proprietà di trasformazione riportate nella tabella in
(2.53) non è tanto la singola ![]() quanto
le forme bilineari negli spinori
quanto
le forme bilineari negli spinori
![]() che si possono
costruire a partire da esse.
che si possono
costruire a partire da esse.
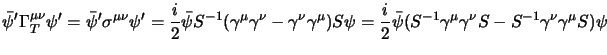


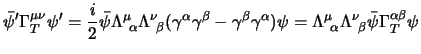
![]() .
.
![]() ; partiamo dalla definizione in
(2.53) usando per
; partiamo dalla definizione in
(2.53) usando per ![]() l'espressione
(2.50); allora si avrà:
l'espressione
(2.50); allora si avrà:

![$\displaystyle \bar \psi' \Gamma_P\psi'=\bar \psi' \gamma^5 \psi'=
\bar \psi \le...
...a\beta\gamma\delta}]
\gamma^\mu\gamma^\nu\gamma^\rho\gamma^\sigma \right)
\psi
$](img808.png)

![]() godono di una serie di proprietà importanti che però non staremo
a dimostrare per intero; è però importante notare che a parte la presenza di
un fattore
godono di una serie di proprietà importanti che però non staremo
a dimostrare per intero; è però importante notare che a parte la presenza di
un fattore ![]() immaginario in alcune di esse possono essere raggruppate in
maniera naturale secondo la seguente tabella (vedi [Mes]):
immaginario in alcune di esse possono essere raggruppate in
maniera naturale secondo la seguente tabella (vedi [Mes]):

![]() ,
, ![]() e
e ![]() ;
in ogni caso guardando alle singoli componenti di 2.1 si
vede subito che qualunque sia il quadrato scelto si avranno sempre due matrici
uguali per ciascun indice diverso, che con un opportuno numero di
anticommutazioni (da cui il segno) potranno essere poste a fianco e quindi
semplificate fino ad arrivare
;
in ogni caso guardando alle singoli componenti di 2.1 si
vede subito che qualunque sia il quadrato scelto si avranno sempre due matrici
uguali per ciascun indice diverso, che con un opportuno numero di
anticommutazioni (da cui il segno) potranno essere poste a fianco e quindi
semplificate fino ad arrivare ![]() .
.
![]() e
e ![]() , per le
altre basta notare che per le
, per le
altre basta notare che per le
![]() si può scegliere la
opportuna
si può scegliere la
opportuna
![]() in modo da avere un prodotto con quattro indici diversi,
ed idem fra le
in modo da avere un prodotto con quattro indici diversi,
ed idem fra le
![]() e poi facendo le opportune anticommutazioni
si ha la proprietà.
e poi facendo le opportune anticommutazioni
si ha la proprietà.
![]() sia
sia
![]() quella che anticommuta, allora si avrà che:
quella che anticommuta, allora si avrà che:
![]() doppie ritornando, eventualmente con un segno opposto, ad
un'altra delle matrici di tab. 2.1 facendo i conti
effettivi si vede anche che con la scelta di
(2.54) il segno è sempre positivo.
doppie ritornando, eventualmente con un segno opposto, ad
un'altra delle matrici di tab. 2.1 facendo i conti
effettivi si vede anche che con la scelta di
(2.54) il segno è sempre positivo.