Abbiamo trovato dunque che anche con l'equazione di Dirac si riottengono le
grane dovute alla presenza di soluzioni ad energia negativa; questo è un
grosso problema, infatti anche se pure in meccanica relativistica classica si
avevano le due radici, quella negativa la si poteva sempre scartare, perché
una particella che avesse energia positiva avrebbe comunque mantenuto anche da
ferma un'energia positiva pari alla sua massa di riposo, non potendo saltare
il gap energetico fra ![]() e
e ![]() ; in meccanica quantistica però le
variazioni di energia possono essere discontinue, e una particella tende
sempre a fare una transizione da uno stato di energia superiore ad uno ad
energia inferiore; e quindi il passaggio agli stati ad energia negativa
sarebbe immediato, e non solo non si potrebbero più eliminare questi stati, ma
tutte le particelle dovrebbero decadere verso di essi e da essi giù giù verso
; in meccanica quantistica però le
variazioni di energia possono essere discontinue, e una particella tende
sempre a fare una transizione da uno stato di energia superiore ad uno ad
energia inferiore; e quindi il passaggio agli stati ad energia negativa
sarebbe immediato, e non solo non si potrebbero più eliminare questi stati, ma
tutte le particelle dovrebbero decadere verso di essi e da essi giù giù verso
![]() . Ovviamente tutto ciò non è accettabile, e si è trovato una
soluzione a questo solo considerando gli stati ad energia negativa come
antiparticelle grazie all'ipotesi del mare di Dirac, la realtà comunque è che
in meccanica quantistica relativistica il concetto di particella singola porta
a dei paradossi e che si può fare una trattazione coerente solo con la teoria
dei campi.
. Ovviamente tutto ciò non è accettabile, e si è trovato una
soluzione a questo solo considerando gli stati ad energia negativa come
antiparticelle grazie all'ipotesi del mare di Dirac, la realtà comunque è che
in meccanica quantistica relativistica il concetto di particella singola porta
a dei paradossi e che si può fare una trattazione coerente solo con la teoria
dei campi.
Abbiamo visto prima come gli spinori nella forma (2.70)
siano autostati dell'operatore quadrimpulso, e come ![]() , autovalore
corrispondente, sia il valore del quadrimpulso di detti stati; questo però non
è del tutto corretto; infatti con la (2.70) otteniamo
dei
, autovalore
corrispondente, sia il valore del quadrimpulso di detti stati; questo però non
è del tutto corretto; infatti con la (2.70) otteniamo
dei ![]() con
con ![]() , ed in tal caso non sarà più immediato considerare
, ed in tal caso non sarà più immediato considerare
![]() come il quadrimpulso di una particella.
come il quadrimpulso di una particella.
Vedremo più avanti che si possono reinterpretare gli stati ad energia negativa
come antiparticelle; se però vogliamo dare a ![]() il significato di un
quadrimpulso dovremo imporre che sia sempre
il significato di un
quadrimpulso dovremo imporre che sia sempre ![]() (questo ci sarà molto
utile in seguito); questo però comporta che la (2.70)
non va più bene per gli stati ad energia negativa; per questo si preferisce
sostituirla con due definizioni separate, una per gli stati ad energia
positiva, ed una, cambiando segno all'esponenziale, per gli stati ad energia
negativa:
(questo ci sarà molto
utile in seguito); questo però comporta che la (2.70)
non va più bene per gli stati ad energia negativa; per questo si preferisce
sostituirla con due definizioni separate, una per gli stati ad energia
positiva, ed una, cambiando segno all'esponenziale, per gli stati ad energia
negativa:

Adesso possiamo vedere cosa ci da l'equazione di Dirac applicata a questi spinori; usiamo l'espressione (2.20) con la notazione di Feynmann, è immediato ottenere che dalla definizione precedente segue:
Per risolvere queste equazioni, considerando il caso di una particella dotata
di massa, ci mettiamo nel sistema solidale nel quale
![]() ed esse si
riducono a:
ed esse si
riducono a:

Queste sono le soluzioni nel sistema solidale, dove la particella è ferma; per
ottenere le soluzioni per un moto qualsiasi basterà fare un boost di Lorentz
su queste ad una velocità
![]() utilizzando le proprietà di
trasformazione per ottenere lo spinore desiderato. Fare i conti con le matrici
di trasformazione però è scomodo, perché bisogna usare
utilizzando le proprietà di
trasformazione per ottenere lo spinore desiderato. Fare i conti con le matrici
di trasformazione però è scomodo, perché bisogna usare
![]() nella
forma generica (2.34), che è un
esponenziale di matrici, il che comporta un calcolo molto complesso con delle
serie di potenze. C'è però un metodo molto più semplice; cominciamo con lo
scriverci il prodotto:
nella
forma generica (2.34), che è un
esponenziale di matrici, il che comporta un calcolo molto complesso con delle
serie di potenze. C'è però un metodo molto più semplice; cominciamo con lo
scriverci il prodotto:
Vediamo anzitutto come effettuare la normalizzazione; evidentemente per non
dannarsi l'anima conviene effettuarla in maniera covariante, in modo che resti
la stessa in tutti i sistemi inerziali; allora dato che sappiamo che
![]() è invariante converrà imporre la normalizzazione su
è invariante converrà imporre la normalizzazione su ![]() e
e
![]() lasciando perdere per ora le questioni relative all'interpretazione
probabilistica. Essendo invariante si può normalizzare nel sistema solidale
usando le soluzioni (2.77) che abbiamo
trovato; presa la definizione (2.40) degli
aggiunti, è banale verificare con un po' di conti che:
lasciando perdere per ora le questioni relative all'interpretazione
probabilistica. Essendo invariante si può normalizzare nel sistema solidale
usando le soluzioni (2.77) che abbiamo
trovato; presa la definizione (2.40) degli
aggiunti, è banale verificare con un po' di conti che:

Adesso bisognerà verificare se gli spinori costruiti con le
(2.80) soddisfano effettivamente queste
relazioni. Calcoliamoci allora le norme, per
![]() sarà:
sarà:
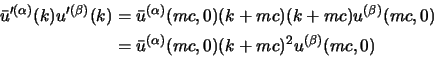
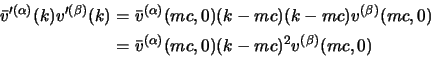
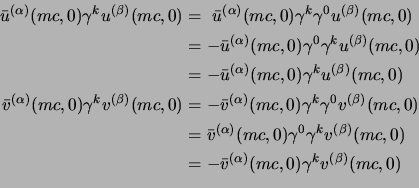
![\begin{displaymath}
\begin{aligned}
&\bar u'^{(\alpha)}(k) u'^{(\beta)}(k)= \ba...
...ha)}(mc,0)[2mc(mc-k_0\gamma^0)] v^{(\beta)}(mc,0)
\end{aligned}\end{displaymath}](img999.png)
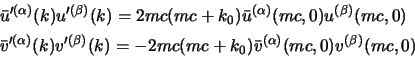
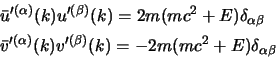
Questi spinori soddisfano le relazioni di ortonormalità; si possono però ottenere da essi anche le relazioni di completezza, consideriamo infatti che, sempre con le espressioni che abbiamo trovato, si ha:
![$\displaystyle \sum_{\alpha=1}^2 \left[
u^{(\alpha)}(mc,0)\bar u^{(\alpha)}(mc,0) -
v^{(\alpha)}(mc,0)\bar v^{(\alpha)}(mc,0)
\right] = \un
$](img1007.png)