




Next: La prova della covarianza
Up: Covarianza dell'equazione di Dirac
Previous: Covarianza dell'equazione di Dirac
Contents
Index
Le proprietà delle matrici

Data la (2.18) si tratta di far vedere che effettivamente si può
considerare l'indice  delle
delle
 come un indice covariante; se
usiamo la rappresentazione di Dirac (2.13)
vista in precedenza possiamo immediatamente esprimere le
come un indice covariante; se
usiamo la rappresentazione di Dirac (2.13)
vista in precedenza possiamo immediatamente esprimere le
 come:
come:
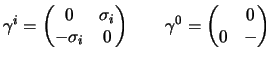 |
(3.19) |
e dato un qualsiasi quadrivettore  si introduce una notazione dovuta a
Feynmann (slash di Feynmann) indicando con
si introduce una notazione dovuta a
Feynmann (slash di Feynmann) indicando con 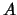 il prodotto
scalare:
così la (2.18) diventa:
il prodotto
scalare:
così la (2.18) diventa:
 |
(3.20) |
e l'identità operatoriale analoga alla (2.4) è 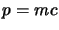 .
.
Le proprietà delle
 si ricavano dalla loro definizione in termini
di
si ricavano dalla loro definizione in termini
di  e delle
e delle 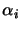 dalle proprietà di quest'ultime; abbiamo già
visto che
dalle proprietà di quest'ultime; abbiamo già
visto che
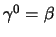 è hermitiana, mentre per le altre si ha che:
è hermitiana, mentre per le altre si ha che:
ma dalle regole di anticommutazione segue che
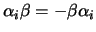 per cui alla fine si ottiene che:
quindi le
per cui alla fine si ottiene che:
quindi le 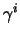 sono antihermitiane; dalla precedente, dato che
sono antihermitiane; dalla precedente, dato che
 , si ottiene anche che:
e dato che questo vale evidentemente anche per
, si ottiene anche che:
e dato che questo vale evidentemente anche per 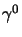 in definitiva si
possono riassumere le precedenti in:
in definitiva si
possono riassumere le precedenti in:
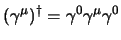 |
(3.21) |
Le proprietà di anticommutazione, che definiscono l'algebra delle
 ,
si ottengono ancora dalle analoghe per
,
si ottengono ancora dalle analoghe per 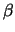 e
e 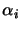 ; cominciamo col
calcolare:
; cominciamo col
calcolare:
qui si può anticommutare 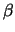 e
e 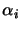 nel secondo membro, ottenendo
immediatamente:
prendiamo poi:
qui si può anticommutare la parte centrale di entrambi gli addendi ottenendo:
infine è immediato che
nel secondo membro, ottenendo
immediatamente:
prendiamo poi:
qui si può anticommutare la parte centrale di entrambi gli addendi ottenendo:
infine è immediato che
 , mentre si ha:
(si noti che non si è usata l'espressione esplicita delle
, mentre si ha:
(si noti che non si è usata l'espressione esplicita delle
 dato che
queste relazioni sono del tutto generali e valide per qualsiasi
rappresentazione); in definitiva si possono riassumere le proprietà di
anticommutazione usando il tensore metrico nell'unica relazione:
dato che
queste relazioni sono del tutto generali e valide per qualsiasi
rappresentazione); in definitiva si possono riassumere le proprietà di
anticommutazione usando il tensore metrico nell'unica relazione:
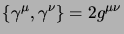 |
(3.22) |
Infine, come per me matrici 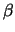 ed
ed 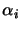 , anche per le
, anche per le
 si possono ottenere altre rappresentazioni diverse dalla
(2.19) attraverso delle trasformazioni unitarie; si
può però dimostrare (non staremo a farlo) anche l'inverso, e cioè che
qualsiasi rappresentazione può essere ottenuta dalla rappresentazione di Dirac
tramite una trasformazione unitaria.
si possono ottenere altre rappresentazioni diverse dalla
(2.19) attraverso delle trasformazioni unitarie; si
può però dimostrare (non staremo a farlo) anche l'inverso, e cioè che
qualsiasi rappresentazione può essere ottenuta dalla rappresentazione di Dirac
tramite una trasformazione unitaria.





Next: La prova della covarianza
Up: Covarianza dell'equazione di Dirac
Previous: Covarianza dell'equazione di Dirac
Contents
Index
Simone Piccardi
2003-02-20
![]() delle
delle
![]() come un indice covariante; se
usiamo la rappresentazione di Dirac (2.13)
vista in precedenza possiamo immediatamente esprimere le
come un indice covariante; se
usiamo la rappresentazione di Dirac (2.13)
vista in precedenza possiamo immediatamente esprimere le
![]() come:
come:
![]() si ricavano dalla loro definizione in termini
di
si ricavano dalla loro definizione in termini
di ![]() e delle
e delle ![]() dalle proprietà di quest'ultime; abbiamo già
visto che
dalle proprietà di quest'ultime; abbiamo già
visto che
![]() è hermitiana, mentre per le altre si ha che:
è hermitiana, mentre per le altre si ha che:
![]() ,
si ottengono ancora dalle analoghe per
,
si ottengono ancora dalle analoghe per ![]() e
e ![]() ; cominciamo col
calcolare:
; cominciamo col
calcolare:
![]() ed
ed ![]() , anche per le
, anche per le
![]() si possono ottenere altre rappresentazioni diverse dalla
(2.19) attraverso delle trasformazioni unitarie; si
può però dimostrare (non staremo a farlo) anche l'inverso, e cioè che
qualsiasi rappresentazione può essere ottenuta dalla rappresentazione di Dirac
tramite una trasformazione unitaria.
si possono ottenere altre rappresentazioni diverse dalla
(2.19) attraverso delle trasformazioni unitarie; si
può però dimostrare (non staremo a farlo) anche l'inverso, e cioè che
qualsiasi rappresentazione può essere ottenuta dalla rappresentazione di Dirac
tramite una trasformazione unitaria.