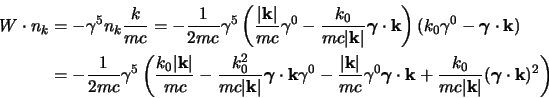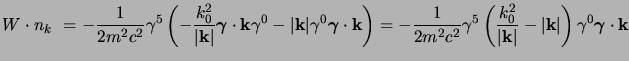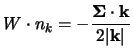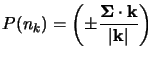Next: La costruzione di una
Up: Le soluzioni di particella
Previous: Gli stati ad energia
Contents
Index
I proiettori su stati di quadrimpulso e spin definito
Avendo trovato le soluzioni in onda piana con le trasformate di Fourier
potremo esprimere in generale una soluzione qualsiasi come sovrapposizione di
stati puri di quadrimpulso; prima di farlo però conviene analizzare meglio il
significato degli spinori
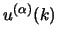 e
e
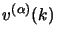 , cercando
anche una relazione con lo spin.
, cercando
anche una relazione con lo spin.
Un primo passo da fare è quello di definire i proiettori relativi a questi
stati a quadrimpulso definito; in analogia al caso della meccanica quantistica
classica in cui il proiettore su uno stato
 è
è
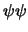 potremo scrivere il proiettore
potremo scrivere il proiettore
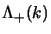 su uno
stato ad energia positiva di quadrimpulso
su uno
stato ad energia positiva di quadrimpulso 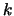 come:
come:
le (2.88) ci mostrano subito le proprietà di proiettore sugli
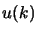 di
di
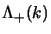 e sui
e sui 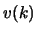 di
di
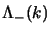 , non sono però una
forma molto comoda da usare nei conti e per questo si cerca una espressione
più agevole; utilizzandole possiamo scrivere:
ma dalle espressioni degli
, non sono però una
forma molto comoda da usare nei conti e per questo si cerca una espressione
più agevole; utilizzandole possiamo scrivere:
ma dalle espressioni degli
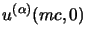 e dei
e dei
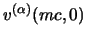 si
può verificare banalmente che:
dunque sostituendo nelle precedenti si ha:
adesso per entrambe il primo addendo in parentesi quadra lo abbiamo dalle
(2.82), resta il secondo che possiamo
sviluppare come:
adesso però
si
può verificare banalmente che:
dunque sostituendo nelle precedenti si ha:
adesso per entrambe il primo addendo in parentesi quadra lo abbiamo dalle
(2.82), resta il secondo che possiamo
sviluppare come:
adesso però
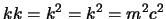 ed il secondo addendo si annulla
con l'ultimo, mentre si può raccogliere l'anticommutatore ottenendo:
ma adesso dalle regole di anticommutazione si ha che:
dunque alla fine:
allora sostituendo questa nelle precedenti espressioni per
ed il secondo addendo si annulla
con l'ultimo, mentre si può raccogliere l'anticommutatore ottenendo:
ma adesso dalle regole di anticommutazione si ha che:
dunque alla fine:
allora sostituendo questa nelle precedenti espressioni per
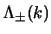 ed usando anche le (2.82) si ottiene che:
dalle quali è immediato ottenere, con un po' di semplificazioni, le espressioni
definitive per i proiettori:
ed usando anche le (2.82) si ottiene che:
dalle quali è immediato ottenere, con un po' di semplificazioni, le espressioni
definitive per i proiettori:
Un modo molto più rapido per ottenere questi risultati è quello di sfruttare
il fatto che gli spinori
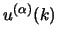 e
e
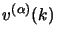 sono una base
nello spazio
sono una base
nello spazio  degli spinori, per cui possiamo applicare il teorema
che dice che se due operatori danno lo stesso risultato applicati ad una base
dello spazio vettoriale su cui operano allora sono lo stesso operatore; dalla
definizione in (2.88), grazie alle relazioni di normalizzazione
(2.81), si ha:
degli spinori, per cui possiamo applicare il teorema
che dice che se due operatori danno lo stesso risultato applicati ad una base
dello spazio vettoriale su cui operano allora sono lo stesso operatore; dalla
definizione in (2.88), grazie alle relazioni di normalizzazione
(2.81), si ha:
ma adesso notiamo che dalle equazioni per gli spinori
(2.76) si ottiene che:
e con queste è banale verificare che le espressioni (2.89)
soddisfano le (2.90) e sono quindi gli operatori
di proiezione.
Le espressioni in (2.89) sono molto comode per verificare le
varie proprietà degli operatori di proiezione; la prima è la proprietà di base
di tutti i proiettori e cioè l'idempotenza:
la cosa si verifica subito con le espressioni (2.89) usando le
(2.82); infatti:
la seconda proprietà ci dice che questi proiettori sono ortogonali, cioè si
ha che:
anche questa si ottiene dalle (2.89); consideriamo la prima,
si avrà:
e allo stesso modo si ottiene che
 . Dato poi che
le
. Dato poi che
le
 sono a traccia nulla si ottiene anche che:
infine se prendiamo le espressioni originali dei proiettori in termini degli
spinori è immediato verificare la proprietà di completezza, cioè che:
ma altrettanto si ottiene con le (2.89) dato che:
sono a traccia nulla si ottiene anche che:
infine se prendiamo le espressioni originali dei proiettori in termini degli
spinori è immediato verificare la proprietà di completezza, cioè che:
ma altrettanto si ottiene con le (2.89) dato che:
Abbiamo così trovato le espressioni e le proprietà dei proiettori sugli stati
di impulso definito ad energia positiva e negativa; ci resta da caratterizzare
l'ulteriore degenerazione degli spinori, che abbiamo visto essere strettamente
legata alla presenza di un momento angolare intrinseco: in sostanza vogliamo
trovare i proiettori per gli stati in cui è definito anche lo spin.
Consideriamo allora il vettore di Pauli-Lubansky, nel nostro caso, avendo
preso spinori ad impulso definito, avremo che
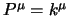 , per cui si
ottiene subito che:
, per cui si
ottiene subito che:
sappiamo però che questo è un vettore ortogonale a 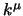 (abbiamo visto
in §2.3.7 che
(abbiamo visto
in §2.3.7 che
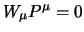 ) allora se cerchiamo un direzione
per il momento angolare intrinseco possiamo prendere un versore
) allora se cerchiamo un direzione
per il momento angolare intrinseco possiamo prendere un versore 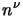 ortogonale a
ortogonale a 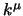 e space-like, cioè tale che:
e con questo potremo caratterizzare lo spin con la proiezione lungo una
qualsiasi delle direzioni che può prendere utilizzando (in maniera analoga al
e space-like, cioè tale che:
e con questo potremo caratterizzare lo spin con la proiezione lungo una
qualsiasi delle direzioni che può prendere utilizzando (in maniera analoga al
 o al
o al
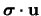 della meccanica classica) la
componente:
(il passaggio si fa sfruttando le proprietà del tensore di Ricci) adesso
possiamo sfruttare la seconda delle (2.55)
per assorbire il tensore di Ricci ottenendo che:
(si è cambiato nome agli indici) consideriamo però che:
della meccanica classica) la
componente:
(il passaggio si fa sfruttando le proprietà del tensore di Ricci) adesso
possiamo sfruttare la seconda delle (2.55)
per assorbire il tensore di Ricci ottenendo che:
(si è cambiato nome agli indici) consideriamo però che:
![$\displaystyle \gamma^\mu\gamma^\nu=\half \{\gamma^\mu,\gamma^\nu \}+\half [\gamma^\mu,\gamma^\nu]=g^{\mu\nu}-i\sigma^{\mu\nu}$](img1047.png) |
(3.91) |
(si sono usate la definizione di
 e le relazioni di
anticommutazione) per cui si può riscrivere la precedente come:
ma adesso il termine in
e le relazioni di
anticommutazione) per cui si può riscrivere la precedente come:
ma adesso il termine in
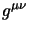 ci da
ci da
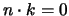 per cui resta:
per cui resta:
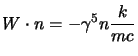 |
(3.92) |
calcoliamo allora il valore di questa proiezione su uno dei nostri spinori ad
impulso definito, usando la relazione (2.76)
si verifica immediatamente che:
Ma adesso, dato che
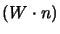 è uno scalare, lo possiamo calcolare dove ci
pare, ed il risultato sarà lo stesso; allora scegliamo di fare il calcolo nel
sistema solidale, e per semplificare i conti consideriamo il caso in cui
è uno scalare, lo possiamo calcolare dove ci
pare, ed il risultato sarà lo stesso; allora scegliamo di fare il calcolo nel
sistema solidale, e per semplificare i conti consideriamo il caso in cui 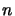 è
il versore che punta lungo l'asse
è
il versore che punta lungo l'asse  , cioè sia
, cioè sia
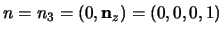 che è evidentemente ortogonale a
che è evidentemente ortogonale a
 . In
questo caso abbiamo visto in §2.3.7 il valore del vettore di
Pauli-Lubansky è dato dalla (2.69); per cui il
valore del prodotto scalare è banalmente:
. In
questo caso abbiamo visto in §2.3.7 il valore del vettore di
Pauli-Lubansky è dato dalla (2.69); per cui il
valore del prodotto scalare è banalmente:
e se usiamo le espressioni (2.68) che avevamo trovato per
 , applicandole alle soluzioni nel sistema solidale
(2.77) è banale verificare che si
ottiene:
(dove si è usato il termine
, applicandole alle soluzioni nel sistema solidale
(2.77) è banale verificare che si
ottiene:
(dove si è usato il termine
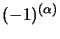 per assorbire il segno meno
di
per assorbire il segno meno
di 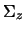 e tener conto automaticamente del cambiamento di segno al
variare di
e tener conto automaticamente del cambiamento di segno al
variare di 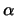 dovuto dalla definizione della matrice di Pauli
dovuto dalla definizione della matrice di Pauli
 ) cioè le nostre soluzioni di
(2.77) sono anche autostati di spin.
) cioè le nostre soluzioni di
(2.77) sono anche autostati di spin.
Ma dato che
 è invariante, questa varrà anche in tutti gli altri
sistemi di riferimento, in cui la particella ha impulso
è invariante, questa varrà anche in tutti gli altri
sistemi di riferimento, in cui la particella ha impulso 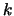 generico, per cui
se
generico, per cui
se 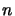 è il trasformato di
è il trasformato di 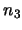 avremo anche che:
avremo anche che:
per cui, dal confronto di questa con la
(2.93), otterremo che, se 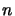 è il versore
che nel sistema di riferimento solidale è orientato lungo l'asse
è il versore
che nel sistema di riferimento solidale è orientato lungo l'asse  , si ha:
, si ha:
Con queste ultime relazioni viene naturale definire il proiettore sugli stati
a spin definito come:
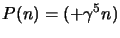 |
(3.96) |
dove 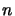 può anche essere un versore generico. In futuro comunque, dato che
può essere usata come osservabile indipendente solo la proiezione lungo una
direzione dello spin, daremo sempre per sottinteso che
può anche essere un versore generico. In futuro comunque, dato che
può essere usata come osservabile indipendente solo la proiezione lungo una
direzione dello spin, daremo sempre per sottinteso che 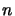 è presa nella
direzione che corrisponde all'asse
è presa nella
direzione che corrisponde all'asse  del sistema di riferimento solidale con
la particella.
del sistema di riferimento solidale con
la particella.
Se ci ricordiamo che i nostri spinori sono una base per lo spazio degli
spinori, possiamo vedere l'effetto su di essi di questo proiettore; usando le
(2.95) è immediato ottenere che:
Con queste definizioni si possono allora caratterizzare i vari spinori della
nostra base in maniera alternativa come
 ,
,
 ,
,
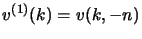 ,
,
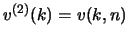 e talvolta si
dice anche che
e talvolta si
dice anche che 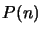 proietta sugli stati a spin up (perchè quello stato ha
ha autovalore 1/2 per
proietta sugli stati a spin up (perchè quello stato ha
ha autovalore 1/2 per 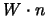 ) per gli stati ad energia positiva e sugli
stati a spin down per gli stati a energia negativa.
) per gli stati ad energia positiva e sugli
stati a spin down per gli stati a energia negativa.
In realtà questa classificazione è impropria, infatti anche se le
(2.94) ci permettono di definire quali sono gli
stati di spin rispetto alla direzione  nel sistema solidale, parlare di
spin up o spin down cosa non immediato perché, avendo a che fare anche con
spinori a norma negativa come i
nel sistema solidale, parlare di
spin up o spin down cosa non immediato perché, avendo a che fare anche con
spinori a norma negativa come i
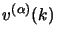 , gli autovalori di
, gli autovalori di 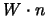 , non corrispondono direttamente alle osservabili fisiche. Occorre
ricordare infatti che queste ultime sono date in generale dal prodotto
, non corrispondono direttamente alle osservabili fisiche. Occorre
ricordare infatti che queste ultime sono date in generale dal prodotto
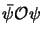 (con
(con  che esprime l'osservabile) perché è
questa la quantità che, espresso
che esprime l'osservabile) perché è
questa la quantità che, espresso 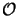 in termini dei covarianti di Dirac
in termini dei covarianti di Dirac
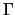 visti in §2.3.6, trasforma correttamente.
visti in §2.3.6, trasforma correttamente.
Nel nostro caso allora
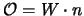 , e per
, e per 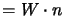 possiamo usare
la (2.93). Con quella possiamo calcolare
possiamo usare
la (2.93). Con quella possiamo calcolare
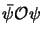 per ciascuno dei nostri spinori usando le
(2.95). In tal caso però otterremo, dato che
secondo le (2.81) è
per ciascuno dei nostri spinori usando le
(2.95). In tal caso però otterremo, dato che
secondo le (2.81) è
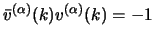 che il valore della proiezione dello spin
che il valore della proiezione dello spin 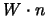 è
è
 per
per
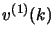 e
e  per
per
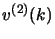 , cioè l'opposto degli
autovalori dell'operatore.
, cioè l'opposto degli
autovalori dell'operatore.
Si noti che la definizione (2.96) è in forma
covariante, ed è molto più comoda perché può essere tranquillamente estesa ad
un 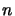 qualunque, nel qual caso
qualunque, nel qual caso 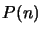 sarà il proiettore sullo stato di spin
orientato nella direzione tale che nel sistema solidale esso avrà
sarà il proiettore sullo stato di spin
orientato nella direzione tale che nel sistema solidale esso avrà
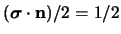 .
.
Adesso possiamo verificare le proprietà di 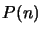 anche per
anche per 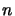 qualsiasi;
anzitutto si può dimostrarne l'idempotenza, cioè che è:
qualsiasi;
anzitutto si può dimostrarne l'idempotenza, cioè che è:
infatti scritto esplicitamente si ha:
ma dato che le
 e
e 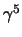 anticommutano si ottiene subito che:
ma adesso sappiamo che
anticommutano si ottiene subito che:
ma adesso sappiamo che
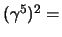 mentre abbiamo visto anche che
mentre abbiamo visto anche che
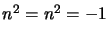 per cui
per cui
 per cui alla fine si ha:
la seconda proprietà di questi proiettori è che sono ortogonali, cioè che:
infatti svolgendo i conti questa diventa:
e per quanto visto prima per cui
per cui alla fine si ha:
la seconda proprietà di questi proiettori è che sono ortogonali, cioè che:
infatti svolgendo i conti questa diventa:
e per quanto visto prima per cui
 si ottiene
subito che questo è nullo; infine è assolutamente banale ottenere la proprietà
di completezza, cioè che:
si ottiene
subito che questo è nullo; infine è assolutamente banale ottenere la proprietà
di completezza, cioè che:
Le proprietà più interessanti di 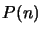 sono comunque quelle che lo legano ai
due proiettori sugli stati ad energia positiva e negativa
sono comunque quelle che lo legano ai
due proiettori sugli stati ad energia positiva e negativa
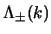 ; si
infatti si hanno le relazioni:
; si
infatti si hanno le relazioni:
si tratta di dimostrare queste proprietà; cominciamo dalla prima; da quanto
visto sappiamo che:
(si sono scartati tutti i termini banalmente commutanti); adesso possiamo
sfruttare la proprietà generale dei commutatori:
nel nostro caso conviene usare gli anticommutatori, per cui la precedente
diventa:
ma 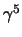 e le
e le
 anticommutano ed il primo addendo si elimina,
mentre per il secondo si può considerare che:
anticommutano ed il primo addendo si elimina,
mentre per il secondo si può considerare che:
 |
(3.99) |
che vale assolutamente in generale qualunque siano 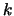 e
e 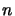 , ma nel nostro
caso sappiamo che
, ma nel nostro
caso sappiamo che
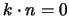 per cui anche il secondo addendo della
precedente si annulla e la (2.98a) è dimostrata.
per cui anche il secondo addendo della
precedente si annulla e la (2.98a) è dimostrata.
La dimostrazione della (2.98b) si ottiene
facilmente se usiamo le proprietà di completezza dei vari proiettori,
infatti si avrà:
Per dimostrare la (2.98c) possiamo scriverci
esplicitamente la traccia come:
ma adesso
 e
e
 dunque il primo ed il secondo addendo sono nulli per la proprietà 3) delle
dunque il primo ed il secondo addendo sono nulli per la proprietà 3) delle
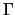 (che hanno tutte, tranne
(che hanno tutte, tranne  , traccia nulla) mentre il terzo è
nella forma
, traccia nulla) mentre il terzo è
nella forma
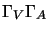 allora per la proprietà 4) questa è ancora una
allora per la proprietà 4) questa è ancora una
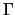 diversa da
diversa da  e quindi anche questo è a traccia nulla; resta così
solo il primo addendo che dimostra banalmente la
(2.98c). Allo stesso modo si può dimostrare che:
e quindi anche questo è a traccia nulla; resta così
solo il primo addendo che dimostra banalmente la
(2.98c). Allo stesso modo si può dimostrare che:
Adesso con questi proiettori, tenendo conto delle
(2.98) si possono definire dei nuovi spinori,
autostati di 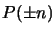 e
e
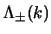 , e base dello spazio degli spinori,
che soddisfino relazioni di ortonormalità e completezza analoghe a quelle
ottenute in precedenza, e questo con
, e base dello spazio degli spinori,
che soddisfino relazioni di ortonormalità e completezza analoghe a quelle
ottenute in precedenza, e questo con 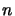 direzione qualsiasi, e non il
trasformato di
direzione qualsiasi, e non il
trasformato di 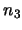 come per gli
come per gli
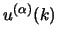 e i
e i
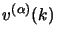 ;
detti spinori sono definiti dalle relazioni:
;
detti spinori sono definiti dalle relazioni:
In tutti i sistemi di riferimento c'è poi una scelta particolare 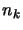 di
di  tale che la parte spaziale n di
tale che la parte spaziale n di  è parallela alla parte spaziale k di
è parallela alla parte spaziale k di 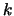 in quel riferimento; se prendiamo infatti il versore:
in quel riferimento; se prendiamo infatti il versore:
si può verificare subito che:
inoltre si ha banalmente:
quindi 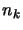 soddisfa le condizioni richieste.
soddisfa le condizioni richieste.
Con questo particolare versore 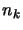 la polarizzazione
la polarizzazione
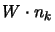 è chiamata
elicità, ed assume un significato particolare, risultando essere la
proiezione dello spin tridimensionale lungo la direzione del moto della
particella; usando le definizioni date si ottiene che:
è chiamata
elicità, ed assume un significato particolare, risultando essere la
proiezione dello spin tridimensionale lungo la direzione del moto della
particella; usando le definizioni date si ottiene che:
adesso però, dato che
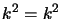 , è immediato ottenere che
, è immediato ottenere che
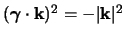 dunque il primo e l'ultimo
termine si semplificano e raccogliendo un
dunque il primo e l'ultimo
termine si semplificano e raccogliendo un  a divisore resta:
dove per l'ultimo passaggio si è anticommutato
a divisore resta:
dove per l'ultimo passaggio si è anticommutato 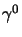 e
e
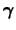 ; adesso si può sostituire a
; adesso si può sostituire a
 ottenendo:
dalla quale, ricordando che
ottenendo:
dalla quale, ricordando che
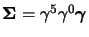 si ottiene la definitiva:
per cui l'elicità
si ottiene la definitiva:
per cui l'elicità  , che si può definire come la proiezione dello spin sulla
direzione del moto è:
, che si può definire come la proiezione dello spin sulla
direzione del moto è:
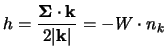 |
(3.100) |
e questa ci mostra subito che  è un invariante.
Si può poi verificare immediatamente che il proiettore:
dove il segno
è un invariante.
Si può poi verificare immediatamente che il proiettore:
dove il segno  è per le soluzioni ad energia positiva ed il segno
è per le soluzioni ad energia positiva ed il segno  per le
soluzioni ad energia negativa) proietta sulle soluzioni ad energia positiva con
elicità positiva e sulle soluzioni ad energia negativa con elicità negativa.
per le
soluzioni ad energia negativa) proietta sulle soluzioni ad energia positiva con
elicità positiva e sulle soluzioni ad energia negativa con elicità negativa.





Next: La costruzione di una
Up: Le soluzioni di particella
Previous: Gli stati ad energia
Contents
Index
Simone Piccardi
2003-02-20
![]() e
e
![]() , cercando
anche una relazione con lo spin.
, cercando
anche una relazione con lo spin.
![]() è
è
![]() potremo scrivere il proiettore
potremo scrivere il proiettore
![]() su uno
stato ad energia positiva di quadrimpulso
su uno
stato ad energia positiva di quadrimpulso ![]() come:
come:
![\begin{displaymath}
\begin{aligned}
\Lambda_+(k)&= {1\over 2m(mc^2+E)} (mc+\s{k...
...(mc,0)\bar v^{(\alpha)}(mc,0)
\right] (mc-\s{k})
\end{aligned}\end{displaymath}](img1016.png)
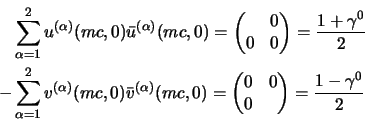
![\begin{displaymath}
\begin{aligned}
\Lambda_+(k)&= {1\over 2m(mc^2+E)}
\left[...
...{k})^2+(mc-\s{k}) \gamma^0 (mc-\s{k})
\right]\cr
\end{aligned}\end{displaymath}](img1018.png)
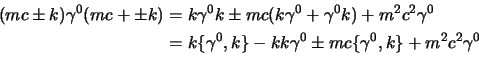


![\begin{displaymath}
\begin{aligned}
\Lambda_+(k) &= {1\over 4m(mc^2+E)}
\left...
...2+E)}
\left[2(mc-\s{k})(mc+{E\over c})\right]\cr
\end{aligned}\end{displaymath}](img1025.png)
![]() e
e
![]() sono una base
nello spazio
sono una base
nello spazio ![]() degli spinori, per cui possiamo applicare il teorema
che dice che se due operatori danno lo stesso risultato applicati ad una base
dello spazio vettoriale su cui operano allora sono lo stesso operatore; dalla
definizione in (2.88), grazie alle relazioni di normalizzazione
(2.81), si ha:
degli spinori, per cui possiamo applicare il teorema
che dice che se due operatori danno lo stesso risultato applicati ad una base
dello spazio vettoriale su cui operano allora sono lo stesso operatore; dalla
definizione in (2.88), grazie alle relazioni di normalizzazione
(2.81), si ha:


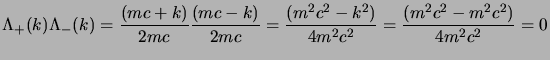
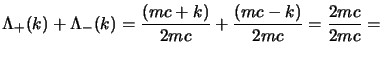
![]() , per cui si
ottiene subito che:
, per cui si
ottiene subito che:
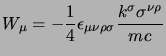
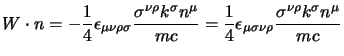
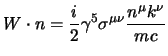
![$\displaystyle W\cdot n={i\over 2}
\gamma^5 [ i(\gamma^\mu\gamma^\nu-g^{\mu\nu})]
{n^\mu k^\nu \over mc}
$](img1048.png)
![]() è uno scalare, lo possiamo calcolare dove ci
pare, ed il risultato sarà lo stesso; allora scegliamo di fare il calcolo nel
sistema solidale, e per semplificare i conti consideriamo il caso in cui
è uno scalare, lo possiamo calcolare dove ci
pare, ed il risultato sarà lo stesso; allora scegliamo di fare il calcolo nel
sistema solidale, e per semplificare i conti consideriamo il caso in cui ![]() è
il versore che punta lungo l'asse
è
il versore che punta lungo l'asse ![]() , cioè sia
, cioè sia
![]() che è evidentemente ortogonale a
che è evidentemente ortogonale a
![]() . In
questo caso abbiamo visto in §2.3.7 il valore del vettore di
Pauli-Lubansky è dato dalla (2.69); per cui il
valore del prodotto scalare è banalmente:
. In
questo caso abbiamo visto in §2.3.7 il valore del vettore di
Pauli-Lubansky è dato dalla (2.69); per cui il
valore del prodotto scalare è banalmente:

![]() è invariante, questa varrà anche in tutti gli altri
sistemi di riferimento, in cui la particella ha impulso
è invariante, questa varrà anche in tutti gli altri
sistemi di riferimento, in cui la particella ha impulso ![]() generico, per cui
se
generico, per cui
se ![]() è il trasformato di
è il trasformato di ![]() avremo anche che:
avremo anche che:
![]() ,
,
![]() ,
,
![]() ,
,
![]() e talvolta si
dice anche che
e talvolta si
dice anche che ![]() proietta sugli stati a spin up (perchè quello stato ha
ha autovalore 1/2 per
proietta sugli stati a spin up (perchè quello stato ha
ha autovalore 1/2 per ![]() ) per gli stati ad energia positiva e sugli
stati a spin down per gli stati a energia negativa.
) per gli stati ad energia positiva e sugli
stati a spin down per gli stati a energia negativa.
![]() nel sistema solidale, parlare di
spin up o spin down cosa non immediato perché, avendo a che fare anche con
spinori a norma negativa come i
nel sistema solidale, parlare di
spin up o spin down cosa non immediato perché, avendo a che fare anche con
spinori a norma negativa come i
![]() , gli autovalori di
, gli autovalori di ![]() , non corrispondono direttamente alle osservabili fisiche. Occorre
ricordare infatti che queste ultime sono date in generale dal prodotto
, non corrispondono direttamente alle osservabili fisiche. Occorre
ricordare infatti che queste ultime sono date in generale dal prodotto
![]() (con
(con ![]() che esprime l'osservabile) perché è
questa la quantità che, espresso
che esprime l'osservabile) perché è
questa la quantità che, espresso ![]() in termini dei covarianti di Dirac
in termini dei covarianti di Dirac
![]() visti in §2.3.6, trasforma correttamente.
visti in §2.3.6, trasforma correttamente.
![]() , e per
, e per ![]() possiamo usare
la (2.93). Con quella possiamo calcolare
possiamo usare
la (2.93). Con quella possiamo calcolare
![]() per ciascuno dei nostri spinori usando le
(2.95). In tal caso però otterremo, dato che
secondo le (2.81) è
per ciascuno dei nostri spinori usando le
(2.95). In tal caso però otterremo, dato che
secondo le (2.81) è
![]() che il valore della proiezione dello spin
che il valore della proiezione dello spin ![]() è
è
![]() per
per
![]() e
e ![]() per
per
![]() , cioè l'opposto degli
autovalori dell'operatore.
, cioè l'opposto degli
autovalori dell'operatore.
![]() qualunque, nel qual caso
qualunque, nel qual caso ![]() sarà il proiettore sullo stato di spin
orientato nella direzione tale che nel sistema solidale esso avrà
sarà il proiettore sullo stato di spin
orientato nella direzione tale che nel sistema solidale esso avrà
![]() .
.
![]() anche per
anche per ![]() qualsiasi;
anzitutto si può dimostrarne l'idempotenza, cioè che è:
qualsiasi;
anzitutto si può dimostrarne l'idempotenza, cioè che è:

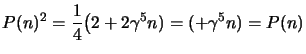
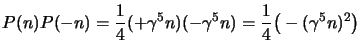
![]() sono comunque quelle che lo legano ai
due proiettori sugli stati ad energia positiva e negativa
sono comunque quelle che lo legano ai
due proiettori sugli stati ad energia positiva e negativa
![]() ; si
infatti si hanno le relazioni:
; si
infatti si hanno le relazioni:
![$\displaystyle [P(n),\Lambda_\pm(k)]
= \left[
\left(
{mc\pm\s{k}\over 2mc}
\r...
...(\un+\gamma^5\s{n})
\right)
\right]
= \pm {1\over 4mc} [\s{k},\gamma^5\s{n}]
$](img1094.png)
![\begin{displaymath}
\begin{aligned}
\left[A, B C \right]
&= [A,B]C + B[A,C] \cr
&= \{ A,B \}C - B\{ A,C \} \cr
\end{aligned}\end{displaymath}](img1095.png)
![$\displaystyle [P(n),\Lambda_\pm(k)]=\pm {1\over 4mc}\left(
\{ \s{k},\gamma^5 \}\s{n}- \gamma^5 \{ \s{k},\s{n}\}\right)
$](img1096.png)
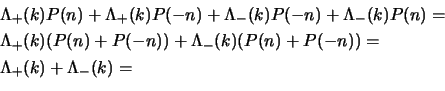
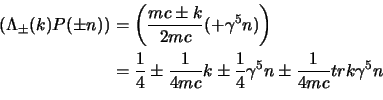
![]() e
e
![]() , e base dello spazio degli spinori,
che soddisfino relazioni di ortonormalità e completezza analoghe a quelle
ottenute in precedenza, e questo con
, e base dello spazio degli spinori,
che soddisfino relazioni di ortonormalità e completezza analoghe a quelle
ottenute in precedenza, e questo con ![]() direzione qualsiasi, e non il
trasformato di
direzione qualsiasi, e non il
trasformato di ![]() come per gli
come per gli
![]() e i
e i
![]() ;
detti spinori sono definiti dalle relazioni:
;
detti spinori sono definiti dalle relazioni:
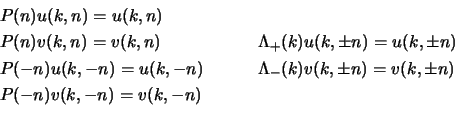
![]() di
di ![]() tale che la parte spaziale n di
tale che la parte spaziale n di ![]() è parallela alla parte spaziale k di
è parallela alla parte spaziale k di ![]() in quel riferimento; se prendiamo infatti il versore:
in quel riferimento; se prendiamo infatti il versore:
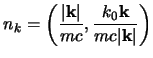

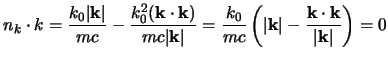
![]() la polarizzazione
la polarizzazione
![]() è chiamata
elicità, ed assume un significato particolare, risultando essere la
proiezione dello spin tridimensionale lungo la direzione del moto della
particella; usando le definizioni date si ottiene che:
è chiamata
elicità, ed assume un significato particolare, risultando essere la
proiezione dello spin tridimensionale lungo la direzione del moto della
particella; usando le definizioni date si ottiene che: