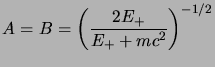Next: Gli stati ad energia
Up: Le soluzioni di particella
Previous: Le soluzioni di particella
Contents
Index
Gli spinori di particella libera
Il metodo di soluzione è quello di usare le trasformate di Fourier, che
permettono di trasformare l'equazione differenziale in un'equazione algebrica;
pertanto si cercano le soluzioni in forma di onda piana:
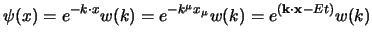 |
(3.70) |
dove tutta la dipendenza dalle coordinate 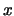 è stata inserita
nell'esponenziale, mentre
è stata inserita
nell'esponenziale, mentre  è uno spinore costante.
è uno spinore costante.
Con questa definizione possiamo vedere che 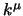 viene ad assumere il
significato di quadrimpulso della particella; dall'equazione di Klein-Gordon
otteniamo infatti banalmente, sostituendovi lo spinore dato dalla
(2.70), la relazione di Einstein
viene ad assumere il
significato di quadrimpulso della particella; dall'equazione di Klein-Gordon
otteniamo infatti banalmente, sostituendovi lo spinore dato dalla
(2.70), la relazione di Einstein
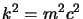 , inoltre
se applichiamo alla (2.70) l'operatore quadrimpulso
(2.64) si ha:
, inoltre
se applichiamo alla (2.70) l'operatore quadrimpulso
(2.64) si ha:
quindi la (2.70) è un autostato dell'operatore
quadrimpulso, con autovalore 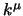 , la (2.70) quindi
descrive gli stati ad impulso definito e l'identificazione di
, la (2.70) quindi
descrive gli stati ad impulso definito e l'identificazione di 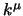 col
quadrimpulso sembra corretta.
col
quadrimpulso sembra corretta.
Il problema nasce quando andiamo a risolvere la (2.18)
esplicitamente, e ritroviamo, come nel caso quasi statico, soluzioni con
energia negativa; vediamo allora come si ottiene questo risultato; scriviamo
al posto di 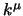 il vettore
il vettore
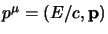 , dall'equazione di Dirac
si ha:
, dall'equazione di Dirac
si ha:
(la si è usata questa forma per comodità); adesso l'esponenziale resta a
fattore e si può semplificare; così, portando tutto a secondo membro si ha:
che è il sistema di equazioni che ci permette di determinare le componenti di
 ; se usiamo la rappresentazione di Dirac è abbastanza semplice trovare:
; se usiamo la rappresentazione di Dirac è abbastanza semplice trovare:
 |
(3.71) |
dove abbiamo indicato con
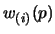 le singole componenti degli spinori
(mettendo l'indice della componente fra parentesi per non confonderlo con gli
altri indici covarianti); questo è un sistema omogeneo, e per avere soluzioni
non banali occorre imporre che il determinante sia nullo; allora posto:
questa condizione è:
questo si calcola al solito modo, e senza stare a fare i conti si ottiene che:
che ha due soluzioni indipendenti:
questo ci dice che per ogni valore di
le singole componenti degli spinori
(mettendo l'indice della componente fra parentesi per non confonderlo con gli
altri indici covarianti); questo è un sistema omogeneo, e per avere soluzioni
non banali occorre imporre che il determinante sia nullo; allora posto:
questa condizione è:
questo si calcola al solito modo, e senza stare a fare i conti si ottiene che:
che ha due soluzioni indipendenti:
questo ci dice che per ogni valore di  solo due delle quattro equazioni del
sistema sono indipendenti; allora potremo fissare arbitrariamente il valore di
due delle quattro componenti di
solo due delle quattro equazioni del
sistema sono indipendenti; allora potremo fissare arbitrariamente il valore di
due delle quattro componenti di  (con la sola condizione di prendere
soluzioni indipendenti) e con quel che resta del sistema determinare le altre
due componenti e definire la soluzione.
(con la sola condizione di prendere
soluzioni indipendenti) e con quel che resta del sistema determinare le altre
due componenti e definire la soluzione.
Troviamo allora l'espressione esplicita dello spinore; cominciamo con il caso
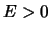 ; qui conviene prendere come condizioni
; qui conviene prendere come condizioni 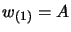 ,
,  e
e
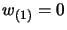 ,
, 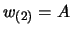 , dato che in tal caso
, dato che in tal caso 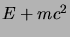 è sicuramente positivo
e diverso da zero, e lo si può dividere nelle ultime due equazioni del sistema
(2.71) ottenendo:
è sicuramente positivo
e diverso da zero, e lo si può dividere nelle ultime due equazioni del sistema
(2.71) ottenendo:
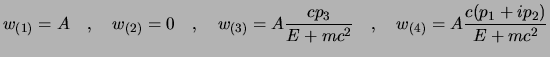 |
(3.72) |
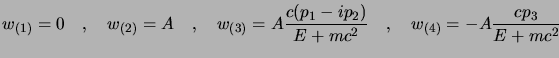 |
(3.73) |
se invece 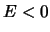 ci conviene prendere
ci conviene prendere  ,
, 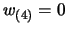 e
e  ,
,
 ed usare le prime due dividendo per
ed usare le prime due dividendo per 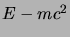 che è sicuramente
negativo e diverso da zero; si ottengono così le altre due soluzioni:
che è sicuramente
negativo e diverso da zero; si ottengono così le altre due soluzioni:
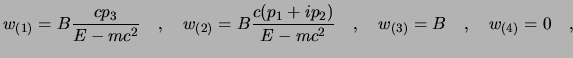 |
(3.74) |
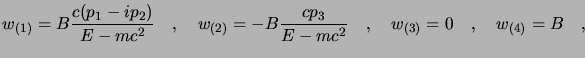 |
(3.75) |
e riassumendo il tutto si scriverà:
tenendo presente che per i primi due 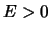 e per i secondi
e per i secondi 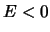 ; si noti
anche come questi si riducano immediatamente all'espressione non relativistica
del §2.2.2 per
; si noti
anche come questi si riducano immediatamente all'espressione non relativistica
del §2.2.2 per 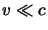 .
.
Un ultimo calcolo è quello della determinazione dei coefficienti 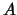 e
e  che
possono essere stabiliti (l'equazione è omogenea) solo dando una
normalizzazione per gli spinori; se chiediamo ad esempio che sia
che
possono essere stabiliti (l'equazione è omogenea) solo dando una
normalizzazione per gli spinori; se chiediamo ad esempio che sia
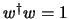 (che è solo una delle normalizzazioni possibili) otterremo che:
(che è solo una delle normalizzazioni possibili) otterremo che:
dove  (non stiamo a fare i conti).
(non stiamo a fare i conti).





Next: Gli stati ad energia
Up: Le soluzioni di particella
Previous: Le soluzioni di particella
Contents
Index
Simone Piccardi
2003-02-20
![]() viene ad assumere il
significato di quadrimpulso della particella; dall'equazione di Klein-Gordon
otteniamo infatti banalmente, sostituendovi lo spinore dato dalla
(2.70), la relazione di Einstein
viene ad assumere il
significato di quadrimpulso della particella; dall'equazione di Klein-Gordon
otteniamo infatti banalmente, sostituendovi lo spinore dato dalla
(2.70), la relazione di Einstein
![]() , inoltre
se applichiamo alla (2.70) l'operatore quadrimpulso
(2.64) si ha:
, inoltre
se applichiamo alla (2.70) l'operatore quadrimpulso
(2.64) si ha:
![]() il vettore
il vettore
![]() , dall'equazione di Dirac
si ha:
, dall'equazione di Dirac
si ha:
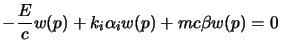
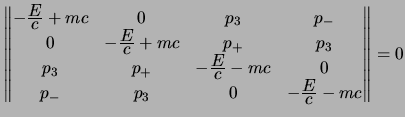

![]() ; qui conviene prendere come condizioni
; qui conviene prendere come condizioni ![]() ,
, ![]() e
e
![]() ,
, ![]() , dato che in tal caso
, dato che in tal caso ![]() è sicuramente positivo
e diverso da zero, e lo si può dividere nelle ultime due equazioni del sistema
(2.71) ottenendo:
è sicuramente positivo
e diverso da zero, e lo si può dividere nelle ultime due equazioni del sistema
(2.71) ottenendo:
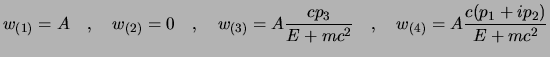
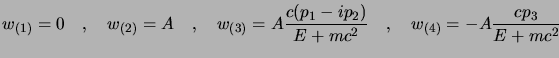
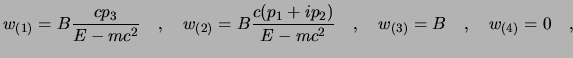
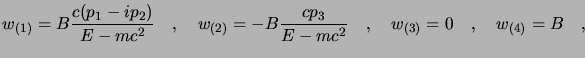
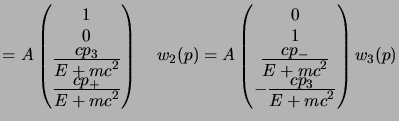
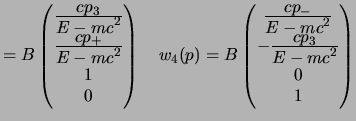
![]() e
e ![]() che
possono essere stabiliti (l'equazione è omogenea) solo dando una
normalizzazione per gli spinori; se chiediamo ad esempio che sia
che
possono essere stabiliti (l'equazione è omogenea) solo dando una
normalizzazione per gli spinori; se chiediamo ad esempio che sia
![]() (che è solo una delle normalizzazioni possibili) otterremo che:
(che è solo una delle normalizzazioni possibili) otterremo che: