Gli operatori di traslazione e rotazione

Prima di cercare le soluzioni dell'equazione di Dirac, conviene esaminare meglio le proprietà del gruppo delle trasformazioni di Poincarè (cioè le trasformazioni di Lorentz più le traslazioni). Per farlo cercheremo l'espressione esplicita dei generatori del gruppo nella rappresentazione che se ne da nello spazio degli spinori.

L'algebra di Lie del gruppo di Poincarè è costituita da 10 generatori, i 4 generatori delle traslazioni che indicheremo con $P^\mu$ e i 6 generatori delle trasformazioni di Lorentz generalizzate (boost e rotazioni) che indicheremo con $M^{\mu\nu}$ (e $M^{\mu\nu}=-M^{\nu\mu}$); le regole di commutazione di tale algebra sono:

dove si sono inseriti gli $\hbar$ per poter considerare $P^\mu$ come operatore di quadrimpulso e $M^{\mu\nu}$ come operatore di momento angolare (relativistico).

Dati i generatori gli operatori di traslazione e rotazione si ottengono esponenziando, e cioè con le espressioni:

dove gli $a^\mu$ sono i parametri della traslazione (il quadrivettore di cui si trasla) mentre $\omega^{\mu\nu}$ sono gli angoli covarianti della trasformazione di Lorentz generalizzata.

Adesso bisogna stare attenti a non confondere questi operatori di trasformazione con le matrici che ci danno la trasformazione delle coordinate; nel caso di trasformazioni di coordinate infatti trasforma il sistema di riferimento, mentre lo spinore, come ente geometrico astratto, resta lo stesso e si va soltanto a cercarne l'espressione in componenti nel nuovo sistema di riferimento. Nel nostro caso invece gli operatori non toccano il sistema di riferimento, ma vanno ad agire sugli spinori trasformandoli punto per punto; però siccome sappiamo come trasformano le componenti degli spinori quando le stesse trasformazioni sono applicate al sistema di riferimento, potremo usare queste proprietà per trovare l'espressione di questi operatori.

Indichiamo allora con $\psi$ lo spinore (qualsiasi) da cui partiamo, inteso come ente geometrico astratto e con $T\psi$ il suo trasformato, mentre con $\psi(x)$ e $T\psi(x)$ indicheremo le componenti di detti spinori in un punto generico di coordinate $x$ del sistema di riferimento (qualsiasi) $S$. Se adesso consideriamo il sistema di riferimento $S'$ ottenuto da $S$ con la stessa trasformazione che abbiamo applicato a $\psi$ in esso otterremo che (avendo trasformato spinore e sistema di riferimento insieme) che le componenti dello spinore $T\psi$ in un punto generico $x$ di $S'$ sono uguali a quelle che ha lo spinore originario $\psi$ nel punto con le stesse coordinate in $S$, il che, in formule, significa:

$$\big(T\psi\big)'(x)=\psi(x)$$ (3.59)

analogamente, se consideriamo la trasformazione inversa, (in questo caso si potrà partire da $S'$ ed $S$ è il sistema trasformato) si otterrà che:

$$T^{-1}\psi(x)=\psi'(x)$$ (3.60)

Adesso per capire a quali trasformazioni si riferiscono gli operatori (2.58) occorre fare qualche passo avanti; le (2.59) e (2.60) infatti sono delle relazioni relazioni fra quantità espresse in sistemi di riferimento diversi e non ci servono a vedere come agiscono gli operatori di trasformazione, perché per vederlo bisogna trovare cos'è lo spinore trasformato rispetto all'originale nello stesso sistema di riferimento. Il fatto di aver usato solo traslazioni e trasformazioni di Lorentz però ci permette, con le espressioni trovate al §2.3.4 per i cambiamenti di sistema di riferimento, di riportare le quantità che nelle (2.59) sono espresse in $S'$ a quelle in $S$.

Cominciamo dalla (2.59); vogliamo trovare $\big(T\psi\big)'(x)$ in $S$; per questo si usa la trasformazione che ci da gli spinori in $S'$ da $S$, ottenendo:

$$\big(T\psi\big)'(x)=S(\Lambda)T\psi(\Lambda^{-1}x)$$

(si ricordi che la trasformazione esprime lo spinore nel punto trasformato, ma noi vogliamo restare nel punto con lo stesso valore valore delle coordinate, per cui occorre partire da $\Lambda^{-1}x$) questa, sostituita nella (2.59), ci da:

$$S(\Lambda)T\psi(\Lambda^{-1}x)=\psi(x)\quad\hbox{cioè}\quad T\psi(\Lambda^{-1}x)=S^{-1}(\Lambda)\psi(x)$$

ma sappiamo che $S^{-1}(\Lambda)=S(\Lambda^{-1})$, inoltre questa, essendo $x$ qualunque, vale anche per $y=\Lambda^{-1}x$ per cui in definitiva si ottiene:

$$T\psi(x)=S(\Lambda^{-1})\psi(\Lambda x)$$ (3.61)

per la (2.60) le cose sono molto più semplici dato che la trasformazione di coordinate ci dice subito che:

$$T^{-1}\psi(x)=S(\Lambda)\psi(\Lambda^{-1}x)$$ (3.62)

Adesso si tratta di stabilire quale delle (2.61) e (2.62) sia da applicare con gli operatori (2.58); ricordiamoci che per definizione essi sono quelli che, assegnato un campo spinoriale qualsiasi (l'analogo di un campo vettoriale, in cui in ogni punto dello spazio è assegnato uno spinore invece di un vettore) prendono lo spinore $\psi$ nel punto $x$ e lo mandano (ruotandolo o traslandolo) nel punto trasformato $\Lambda x$; allora lo spinore trasformato è quello che ha le componenti $S(\Lambda)\psi(x)$ nel punto trasformato $\Lambda x$, ma dalla (2.62) è evidente che:

$$T^{-1}\psi(\Lambda x)=S(\Lambda)\psi(x)$$

quindi è $T^{-1}$ che agisce nel modo voluto; per questo useremo la (2.62) sostituendovi gli operatori (2.58) che scritti in forma infinitesima sono:

cominciamo con le traslazioni; essendo $\Lambda x = x +\Delta a$ si avrà:

$$\left(1+ {i\over\hbar} P^\mu \Delta a_\mu \right) \psi(x) =\psi(x-\Delta a)$$

ma sviluppando il secondo membro in serie di Taylor fino al primo ordine si ottiene:

$$\left(1+ {i\over\hbar} P^\mu \Delta a_\mu \right) \psi(x) = (1-\Delta a_\mu\partial^\mu ) \psi(x)$$

per cui semplificando in ambo i membri il primo addendo si ottiene:

$${i\over\hbar} P^\mu \Delta a_\mu \psi(x) =-\Delta a_\mu\partial^\mu \psi(x)$$

e siccome $\psi(x)$ è qualsiasi possiamo eguagliare direttamente:

$${i\over\hbar} P^\mu \Delta a_\mu =-\Delta a_\mu\partial^\mu$$

ed infine, essendo i $\Delta a_\mu$ arbitrari si ha l'equazione:

$$P^\mu = i \hbar\partial^\mu$$ (3.64)

come appunto ci aspettavamo.

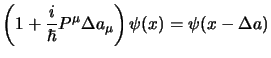
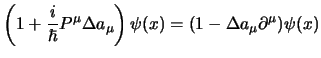
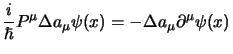
Adesso possiamo esaminare le rotazioni; in questo caso dovremo ricordarci le espressioni per le trasformazioni infinitesime delle coordinate (2.28) e degli spinori (2.29) trovate al § 2.3.2; si otterrà così:

$$\left(1-{i\over 2} J^{\mu\nu}\Delta \omega_{\mu\nu} \right)\psi(x... ...{\mu\nu}\Delta \omega_{\mu\nu} \right) \psi(x^\mu-\Delta \omega^\mu_\nu x^\nu)$$

al solito sviluppiamo in serie di Taylor lo spinore a secondo membro, sarà:

$$\psi(x^\mu-\Delta \omega^\mu_\nu x^\nu)= \psi(x)-(\Delta \omega^\... ...^\nu\partial_\mu )\psi(x)= (1-\Delta \omega^\mu_\nu x^\nu\partial_\mu )\psi(x)$$

che sostituita nella precedente ci da:

$$\left(1-{i\over 2} J^{\mu\nu}\Delta \omega_{\mu\nu} \right)\psi(x... ...ta \omega_{\mu\nu} \right) (1-\Delta \omega^\mu_\nu x^\nu\partial_\mu )\psi(x)$$

da questa, tralasciando i termini di ordine superiore, si ottiene:

$$\left(1-{i\over 2} J^{\mu\nu}\Delta \omega_{\mu\nu} \right)\psi(x... ...Delta \omega_{\mu\nu} -\Delta \omega_\nu^\mu x^\nu\partial_\mu \right)\psi(x)$$

qui al solito il primo addendo di ciascun membro si semplifica, e, come prima, essendo lo spinore qualsiasi, si può semplificare pure lui, resta così l'espressione operatoriale:

$${i\over 2} J^{\mu\nu}\Delta \omega_{\mu\nu}= {i\over 4} \sigma^{\mu\nu}\Delta \omega_{\mu\nu} +\Delta \omega_{\mu\nu} x^\nu \partial^\mu$$

ma scritta così i coefficienti dei $\Delta \omega_{\mu\nu}$ non sono indipendenti perché $x^\nu \partial^\mu$ al contrario degli altri non è un fattore antisimmetrico; allora per poter semplificare i $\Delta \omega_{\mu\nu}$ si deve simmetrizzare; è banale così ottenere che:

$$J^{\mu\nu}=\half \sigma^{\mu\nu}+i(x^\mu\partial^\nu -x^\nu \partial^\mu )$$ (3.65)

e si noti che adesso, oltre al momento angolare orbitale, dato. per analogia col caso tridimensionale, da $M_{orb}^{\mu\nu}= x^\mu P^\nu-x^\nu P^\mu$, si ha pure un momento angolare intrinseco dovuto al termine in $\sigma^{\mu\nu}$.

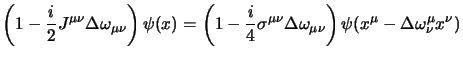
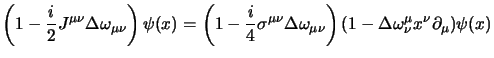
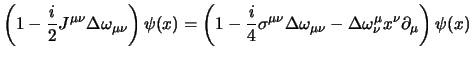
Come nel caso tridimensionale il momento angolare non è invariante per traslazione in quanto è evidente che questo, per una traslazione $a^\mu$ acquista un termine $a^\mu P^\nu -a^\nu P^\mu$, mentre non c'è nessun effetto sul momento angolare intrinseco; per avere un vettore connesso solo a quest'ultimo allora si costruisce il vettore di Pauli-Lubansky:

$$W_\alpha=- \half \epsilon_{\alpha\beta\gamma\delta}{J^{\beta\gamma}P^\delta \over \sqrt{P^\mu P_\mu}}$$ (3.66)

e adesso è banale verificare che la parte orbitale del momento non da più contributo; infatti essa da luogo ad un termine del tipo:

$$x^\beta P^\gamma P^\delta - x^\gamma P^\beta P^\delta$$

ma evidentemente i prodotti $P^\gamma P^\delta$ e $P^\beta P^\delta$, per le loro proprietà di commutazione, sono simmetrici ed essendo contratti col tensore di Ricci, che invece è antisimmetrico, questi fattori si annullano identicamente; inoltre, dato che abbiamo visto che gli spinori soddisfano l'equazione di Klein-Gordon, possiamo scrivere $P^2=m^2c^2$ come identità operatoriale (sottintenderemo da qui in avanti la matrice $\un$ quando ci riferiamo ad operatori multipli dell'unità); allora un'espressione equivalente alla (2.66) è:

$$W_\mu = -{1\over 4} \epsilon_{\mu\nu\rho\sigma} {\sigma^{\nu\rho}... ...\over 4} \epsilon_{\mu\nu\rho\sigma} {\sigma^{\nu\rho}\partial^\sigma \over mc}$$ (3.67)

se andiamo nel sistema solidale poi otteniamo un importante risultato; in tal caso infatti avremo che $P^\mu=(mc,0)$ per cui è:

$$W_\mu^\circ=-{1\over 4}\epsilon_{\mu\nu\rho 0}\sigma^{\nu\rho}$$

allora dato che $\epsilon_{\mu\nu\rho\sigma}$ è nullo se due indici sono uguali si ottiene immediatamente che $W_0^\circ=0$; se poi usiamo la rappresentazione di Dirac per le $\sigma^{\nu\rho}$ si ottiene che:

$$W_i^\circ=-\half \Sigma_i$$

dove $\Sigma_i$ è la componente del vettore:

$$\boldsymbol{\Sigma}=\gamma^5\gamma^0\boldsymbol{\gamma}= \begin{pmatrix}\boldsymbol{\sigma}&0\cr 0&\boldsymbol{\sigma}\cr \end{pmatrix}$$ (3.68)

per cui alla fine:

$$W_\mu^\circ=\left(0,-\half \ssigma \right)$$ (3.69)

si ottiene cioè che la parte spaziale di questo vettore ci da direttamente il vettore di spin (tridimensionale). Dalla definizione (2.67) di $W_\mu$ poi segue subito, per la simmetria del prodotto $P^\sigma P^\mu$, che:

$$W_\mu P^\mu=0$$

(la cosa si ottiene anche in modo diretto usando le espressioni di detti vettori nel sistema solidale), questo ci permette di dire che in qualche modo lo spin è orientato ``ortogonalmente'' alla direzione del moto, ma non certo nel senso che ${\bf p}\cdot \boldsymbol{\sigma}=0$.

La quantità più interessante non è però $W_\mu$ quanto il suo modulo quadro $W^2$ che è il secondo operatore di Casimir del gruppo di Poincarè (il primo è $P^2$); dalla teoria dei gruppi allora otteniamo che ogni rappresentazione di tale gruppo su uno spazio vettoriale è caratterizzata da un valore preciso di questi due operatori; nel caso di $P^2$ sappiamo già che per l'equazione di Dirac esso fissa la massa della particella; vedremo che per $W^2$ otterremo lo spin; nel nostro caso per calcolarlo si può andare nel sistema solidale, nel quale conosciamo l'espressione di $W_\mu$; si ha così:

$$W^2=-{1\over 4} (\Sigma_1^2+ \Sigma_2^2+ \Sigma_3^2)$$

ma per le proprietà delle matrici di Pauli (ed anche dall'espressione (2.68) in termini delle $\gamma$) è banale verificare che $\Sigma_i^2=\un$ per cui alla fine si ha:

$$W^2={3\over 4}=\half\left(\half+1\right)$$

e quindi se prendiamo per $W^2$ l'espressione generale:

$$W^2=s(s+1)$$

si vede subito che i nostri spinori descrivono particelle di spin 1/2.