




Next: I covarianti di Dirac
Up: Covarianza dell'equazione di Dirac
Previous: La quadricorrente
Contents
Index
Le trasformazioni improprie
Si è già accennato a suo tempo che la dimostrazione della covarianza
dell'equazione di Dirac fatta al §2.3.2 vale solo per le
trasformazioni di Lorentz proprie, cioè per le trasformazioni connesse con
l'identità; ci interessa ora vedere cosa accade per le trasformazioni di
Lorentz improprie.
In generale si può sempre scomporre una trasformazione di Lorentz impropria
nel prodotto di una trasformazione di Lorentz propria per una delle tre
trasformazioni improprie di base:
 |
(3.43) |
le cui matrici di trasformazione sono:
 |
(3.44) |
e si noti che anche la terza può essere espressa come il prodotto delle prime
due, quindi non interessa direttamente.
Della prima, che è anche detta time reversal ci occuperemo più
avanti, dato che l'inversione temporale comporta nella realtà anche
l'inversione della dinamica e le cose non sono affatto immediate; per la
parità non ci resta che riscriverci la (2.25) con
l'espressione appena data e si ottiene, chiamata
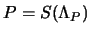 :
:
ma adesso basta notare che a secondo membro non si hanno altro che le
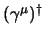 per cui se usiamo la (2.21)
possiamo scrivere:
per cui alla fine si ricava:
dove
per cui se usiamo la (2.21)
possiamo scrivere:
per cui alla fine si ricava:
dove 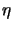 però non potrà essere un numero qualsiasi perché abbiamo
normalizzato imponendo che sia
però non potrà essere un numero qualsiasi perché abbiamo
normalizzato imponendo che sia 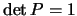 ; per cui potrà essere
; per cui potrà essere
 , ed in generale si usa scrivere la matrice di trasformazione
come:
, ed in generale si usa scrivere la matrice di trasformazione
come:
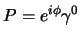 |
(3.45) |
e la scelta dei quattro valori per il fattore di fase è ininfluente dato che
l'unica condizione fisica che si può richiedere è che quattro
riflessioni riportino lo spinore in se stesso, in analogia con le rotazioni dei
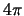 radianti.
radianti.
Dalla (2.45) è evidente che
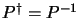 . Si noti infine che il limite non relativistico degli
spinori è un autostato di
. Si noti infine che il limite non relativistico degli
spinori è un autostato di 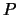 e che gli stati ad energia positiva e negativa
hanno autovalore opposto, cioè, come si suol dire, opposta parità
intrinseca.
e che gli stati ad energia positiva e negativa
hanno autovalore opposto, cioè, come si suol dire, opposta parità
intrinseca.
Infine si può notare che dalla (2.45) è
evidente che 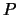 che soddisfa la solita equazione per i coniugati delle
trasformazioni; la formula può essere dimostrata però in maniera del tutto
generale prendendo la coniugata della (2.25):
che soddisfa la solita equazione per i coniugati delle
trasformazioni; la formula può essere dimostrata però in maniera del tutto
generale prendendo la coniugata della (2.25):
adesso in questa si può usare la (2.21), e tenendo
conto che
 si ha:
e questa moltiplicando a destra e a sinistra per
si ha:
e questa moltiplicando a destra e a sinistra per 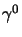 diventa:
e ora si può riutilizzare la (2.25) per il primo
membro ottenendo:
vale a dire, moltiplicando a sinistra per
diventa:
e ora si può riutilizzare la (2.25) per il primo
membro ottenendo:
vale a dire, moltiplicando a sinistra per 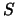 e a destra per
e a destra per 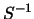 :
ma siccome
:
ma siccome
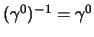 è evidente che:
per cui in definitiva si ottiene:
vale a dire che:
cioè la matrice
è evidente che:
per cui in definitiva si ottiene:
vale a dire che:
cioè la matrice
 commuta con
tutte le
commuta con
tutte le
 , per cui, per il lemma di Shur che dice che quando un
elemento commuta con tutti gli elementi dell'algebra deve essere un multiplo
dell'unità, si ha:
, per cui, per il lemma di Shur che dice che quando un
elemento commuta con tutti gli elementi dell'algebra deve essere un multiplo
dell'unità, si ha:
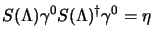 |
(3.46) |
e adesso 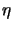 non può essere qualsiasi perché dato che tutti i determinanti
di
non può essere qualsiasi perché dato che tutti i determinanti
di 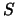 ,
,  e delle
e delle
 sono unitari deve essere:
per cui si ha che
sono unitari deve essere:
per cui si ha che
 ; però la coniugata della
(2.46) ci dice che:
che moltiplicata a sinistra per
; però la coniugata della
(2.46) ci dice che:
che moltiplicata a sinistra per 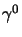 ci da:
mentre la (2.46) moltiplicata a destra per
ci da:
mentre la (2.46) moltiplicata a destra per
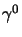 ci dà:
per cui è
ci dà:
per cui è
 e quindi
e quindi
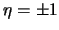 .
.
Adesso, se ricapitoliamo quanto fin qui ottenuto, possiamo ottenere
l'espressione che cercavamo partendo ancora dalla
(2.46) moltiplicata a sinistra 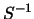 e per
e per
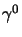 e a destra per
e a destra per 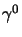 , si ha:
, si ha:
 |
(3.47) |
e possiamo anche determinare definitivamente il segno; per farlo consideriamo
la traccia:
evidentemente questo è un operatore hermitiano e positivo, quindi la traccia
deve essere positiva; però si può scrivere:
ma dalla (2.47) si ha
 dunque:
e adesso possiamo sfruttare la (2.25) con
dunque:
e adesso possiamo sfruttare la (2.25) con 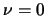 per cui alla fine:
dunque presa la traccia si ha:
ma abbiamo visto al paragrafo §2.2.2 che le
per cui alla fine:
dunque presa la traccia si ha:
ma abbiamo visto al paragrafo §2.2.2 che le 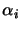 hanno tutte traccia nulla,
quindi alla fine resta:
così se
hanno tutte traccia nulla,
quindi alla fine resta:
così se
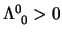 si ha
si ha 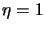 , mentre se
, mentre se
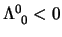 si ha
si ha
 , e questo avviene quando c'è inversione temporale.
, e questo avviene quando c'è inversione temporale.





Next: I covarianti di Dirac
Up: Covarianza dell'equazione di Dirac
Previous: La quadricorrente
Contents
Index
Simone Piccardi
2003-02-20

![]() :
:
![]() . Si noti infine che il limite non relativistico degli
spinori è un autostato di
. Si noti infine che il limite non relativistico degli
spinori è un autostato di ![]() e che gli stati ad energia positiva e negativa
hanno autovalore opposto, cioè, come si suol dire, opposta parità
intrinseca.
e che gli stati ad energia positiva e negativa
hanno autovalore opposto, cioè, come si suol dire, opposta parità
intrinseca.
![]() che soddisfa la solita equazione per i coniugati delle
trasformazioni; la formula può essere dimostrata però in maniera del tutto
generale prendendo la coniugata della (2.25):
che soddisfa la solita equazione per i coniugati delle
trasformazioni; la formula può essere dimostrata però in maniera del tutto
generale prendendo la coniugata della (2.25):
![]() e per
e per
![]() e a destra per
e a destra per ![]() , si ha:
, si ha: