




Next: Il campo di Klein-Gordon.
Up: I campi classici.
Previous: I campi classici.
Contents
Index
Il campo elettromagnetico.
Il primo caso a cui vogliamo applicare quanto visto nei precedenti paragrafi è
quella di una teoria di campo ben nota classicamente come quella
dell'elettromagnetismo; si tratterà di farne emergere la trattazione col
metodo della teoria dei campi relativistica appena mostrato.
Vediamo allora come sviluppare una trattazione lagrangiana relativistica
completa del campo elettromagnetico. Al
§1.4 abbiamo già visto come si
esprimono in forma covariante le equazioni di Maxwell nel sistema di Gauss,
per la teoria dei campi però è più utile il sistema di Heaviside-Lorentz in
cui esse si semplificano in:
partendo dalla stessa espressione (1.76) per il tensore
elettromagnetico
 con un procedimento identico possiamo ottenere
da queste equazioni classiche la corrispondente espressione in forma
relativistica, che è:
con un procedimento identico possiamo ottenere
da queste equazioni classiche la corrispondente espressione in forma
relativistica, che è:
dove
 è il duale del tensore elettromagnetico, definito
secondo la (1.29), già introdotto anche nella
formulazione relativistica dell'elettromagnetismo svolta in
§1.4.
è il duale del tensore elettromagnetico, definito
secondo la (1.29), già introdotto anche nella
formulazione relativistica dell'elettromagnetismo svolta in
§1.4.
A queste va aggiunta la conservazione della carica si esprime ancora con
l'equazione di continuità
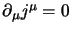 . Come già detto queste equazioni
covarianti esprimono l'invarianza relativistica delle leggi
dell'elettromagnetismo: due importanti invarianti connessi col campo
elettromagnetico, che si ottengono immediatamente dalle contrazioni del
tensore elettromagnetico, sono allora:
. Come già detto queste equazioni
covarianti esprimono l'invarianza relativistica delle leggi
dell'elettromagnetismo: due importanti invarianti connessi col campo
elettromagnetico, che si ottengono immediatamente dalle contrazioni del
tensore elettromagnetico, sono allora:
per esprimere le leggi dell'elettromagnetismo nei termini di una teoria del
campo elettromagnetico ci occorre allora individuare quali sono le variabili
di configurazione e la lagrangiana.
Ad un primo approccio sembrerebbe naturale usare come variabili di
configurazione i campi
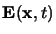 e
e
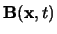 , ma le
equazioni di Maxwell, che dovremmo riottenere dalla teoria, sono del primo
ordine, mentre le equazioni di Eulero del §4.2 sono del
secondo ordine, inoltre in un tal modo otterremmo anche grosse difficoltà a
far emergere in modo naturale la covarianza del procedimento.
, ma le
equazioni di Maxwell, che dovremmo riottenere dalla teoria, sono del primo
ordine, mentre le equazioni di Eulero del §4.2 sono del
secondo ordine, inoltre in un tal modo otterremmo anche grosse difficoltà a
far emergere in modo naturale la covarianza del procedimento.
Per questo motivo si introduce il quadripotenziale 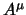 col quale si
possono trasformare le equazioni di Maxwell del primo ordine in un insieme di
equazioni equivalenti del secondo ordine; abbiamo già visto che i campi si
possono esprimere nella forma:
col quale si
possono trasformare le equazioni di Maxwell del primo ordine in un insieme di
equazioni equivalenti del secondo ordine; abbiamo già visto che i campi si
possono esprimere nella forma:
 |
(5.23) |
ed in prossimità di un punto, preso come origine, si può esprimere il
quadripotenziale come:
sappiamo poi che il quadripotenziale non è definito univocamente, ma a meno di
un gradiente di una qualsiasi funzione, il che permette di definire le
trasformazioni di gauge come:
usando la divergenza del tensore elettromagnetico, dalla definizione
(4.23), si può ottenere l'equazione per il quadripotenziale
che è equivalente alle equazioni di Maxwell; si ha:
che si scrive in forma compatta come:
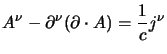 |
(5.24) |
che è manifestamente invariante per trasformazioni di gauge, come si può
verificare con una sostituzione.
L'arbitrarietà connessa alla scelta della condizione di gauge permette allora
di semplificare enormemente i calcoli, ma in certi casi può anche distruggere
la covarianza manifesta delle equazioni; se scriviamo esplicitamente la
(4.24) otteniamo:
che sono piuttosto complicate, per cui la scelta di una opportuna condizione
di gauge può essere di grande aiuto.
Consideriamo come esempio l'uso della gauge di Poisson (
 ); essa
permette di eliminare ogni derivata rispetto al tempo dalla prima di queste
due equazioni, che diventa così un vincolo indipendente dal tempo, e permette
di determinare il potenziale come:
); essa
permette di eliminare ogni derivata rispetto al tempo dalla prima di queste
due equazioni, che diventa così un vincolo indipendente dal tempo, e permette
di determinare il potenziale come:
per cui poi solo il potenziale vettore viene ad obbedire ad una equazione delle
onde che è:
la trattazione è perfettamente coerente e viene usata spesso quando si fanno
studi di interazione del campo elettromagnetico con sistemi legati; essa
presenta poi l'enorme vantaggio di aver rimosso ogni ulteriore arbitrarietà dei
potenziali, ma in questo modo si perde completamente la covarianza
manifesta della teoria.
La gauge più usata però è quella di Lorentz in cui
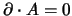 . Questa
ha il grande pregio di mantenere manifesta la covarianza della teoria e di
semplificare le (4.24), dando luogo a delle equazioni (le
equazioni delle onde trovate al §1.4)
identiche per tutte le componenti dei potenziali; essa però, come vedremo in
seguito, non rimuove completamente l'arbitrarietà dei potenziali.
. Questa
ha il grande pregio di mantenere manifesta la covarianza della teoria e di
semplificare le (4.24), dando luogo a delle equazioni (le
equazioni delle onde trovate al §1.4)
identiche per tutte le componenti dei potenziali; essa però, come vedremo in
seguito, non rimuove completamente l'arbitrarietà dei potenziali.
Vogliamo dunque trovare una formulazione lagrangiana invariante per la teoria
dell'elettromagnetismo, per usare quanto visto ai precedenti paragrafi; allora
cercheremo anzitutto l'espressione della lagrangiana del campo
elettromagnetico in termine dei potenziali 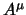 . Questo però comporta un
problema; sappiamo infatti che i potenziali non sono delle quantità
osservabili direttamente, dato che dipendono dalla scelta della gauge; questo
causerà delle difficoltà nella quantizzazione perché essi non possono essere
considerati come variabili dinamiche indipendenti; per ora comunque ci
limiteremo a cercare un'espressione per la densità di lagrangiana
. Questo però comporta un
problema; sappiamo infatti che i potenziali non sono delle quantità
osservabili direttamente, dato che dipendono dalla scelta della gauge; questo
causerà delle difficoltà nella quantizzazione perché essi non possono essere
considerati come variabili dinamiche indipendenti; per ora comunque ci
limiteremo a cercare un'espressione per la densità di lagrangiana 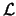 del
campo elettromagnetico con la quale poi esprimere anche le altre quantità
misurabili.
del
campo elettromagnetico con la quale poi esprimere anche le altre quantità
misurabili.
Per trovare 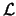 partiamo dal fatto che sappiamo che il quadripotenziale
partiamo dal fatto che sappiamo che il quadripotenziale
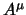 è un quadrivettore, mentre ci occorre uno scalare invariante funzione
di esso e delle sue derivate prime. L'invarianza di gauge delle equazioni del
moto non comporta automaticamente anche quella della lagrangiana; sappiamo
infatti che tutte le possibili scelte di una lagrangiana a meno della
quadridivergenza di una funzione qualunque danno luogo alle stesse equazioni
del moto, per cui dall'invarianza di gauge otteniamo solo l'ulteriore
richiesta che per trasformazioni di gauge dei potenziali la lagrangiana debba
avere al più una divergenza aggiuntiva.
è un quadrivettore, mentre ci occorre uno scalare invariante funzione
di esso e delle sue derivate prime. L'invarianza di gauge delle equazioni del
moto non comporta automaticamente anche quella della lagrangiana; sappiamo
infatti che tutte le possibili scelte di una lagrangiana a meno della
quadridivergenza di una funzione qualunque danno luogo alle stesse equazioni
del moto, per cui dall'invarianza di gauge otteniamo solo l'ulteriore
richiesta che per trasformazioni di gauge dei potenziali la lagrangiana debba
avere al più una divergenza aggiuntiva.
La cosa più semplice è allora prendere una lagrangiana quadratica nei
potenziali e nelle loro derivate; in questo caso la forma più generale che
possiamo prendere con la condizione di avere un invariante è (per snellire la
notazione useremo nel resto del paragrafo le unità naturali per cui 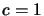 ):
):
e da questa vogliamo ottenere le equazioni del moto (4.24)
tramite le equazioni di Eulero che in questo caso possiamo scrivere come:
avendo introdotto per snellire le formule la notazione
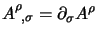 , con la quale la precedente
lagrangiana si scrive come:
calcoliamoci allora le derivate dei singoli pezzi della lagrangiana: dato che
i primi tre dipendono solo dalle derivate dei campi il primo termine della
contiene solo gli ultimi due; viceversa il secondo termine dipenderà solo dai
primi tre.
, con la quale la precedente
lagrangiana si scrive come:
calcoliamoci allora le derivate dei singoli pezzi della lagrangiana: dato che
i primi tre dipendono solo dalle derivate dei campi il primo termine della
contiene solo gli ultimi due; viceversa il secondo termine dipenderà solo dai
primi tre.
Cominciamo dalle derivate rispetto alle variabili canoniche (cioè i
quadripotenziali  ) usando la relazione base
) usando la relazione base
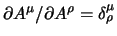 ; il primo termine da esaminare è:
; il primo termine da esaminare è:
il secondo pezzo è ancora più facile da ottenere:
le derivate delle derivate dei campi sono invece un po' più delicate da
fare, e bisogna stare attenti a non fare confusione con gli indici, la
relazione base infatti è:
cominciamo allora col primo termine contenente le derivate dei potenziali, si
avrà:
adesso qui avendo gli indici contratti non è immediatamente chiaro come
fare le derivate, scriviamoci perciò
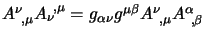 e adesso avendo
tutto in termini di indici diversi potremo derivare rispetto alle
e adesso avendo
tutto in termini di indici diversi potremo derivare rispetto alle
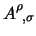 ottenendo:
il secondo termine nelle derivate lo trattiamo allo stesso modo;
riscrivendoci anzitutto
ottenendo:
il secondo termine nelle derivate lo trattiamo allo stesso modo;
riscrivendoci anzitutto
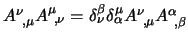 , dunque si ha:
per l'ultimo termine nelle derivate scriviamoci
, dunque si ha:
per l'ultimo termine nelle derivate scriviamoci
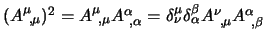 , per cui:
, per cui:
e sostituendo tutte queste nella precedente espressione tentativa per la
lagrangiana ed applicando le equazioni di Eulero-Lagrnage si ottengono le
equazioni del moto che sono:
in questa poi si può notare che gli ultimi due addendi, dato che l'indice
su cui si somma può è muto e le derivate commutano, danno due termini identici
da poter raccogliere, per cui dal confronto di questa con la
(4.24) si ottiene banalmente che 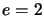 ,
, 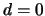 ,
, 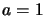 e
e 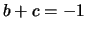 ,
e con questi valori, sostituendo
,
e con questi valori, sostituendo 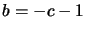 si può riscrivere la lagrangiana
come:
si può riscrivere la lagrangiana
come:
![$\displaystyle {\cal L} = \half \big( \partial_\mu A^\nu \partial^\mu A_\nu - \p...
...rtial_\mu A^\mu)^2 -\partial_\mu A^\nu \partial_\nu A^\mu ] \big) + j^\mu A_\mu$](img1878.png) |
(5.26) |
e qui possiamo abbassare e alzare gli indici nei primi due addendi
ottenendo:
adesso però consideriamo che:
e qui basta cambiare nome agli indici, che tanto sono muti, per ottenere che:
che sostituita nella precedente espressione di 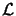 ci porta alla
espressione:
ci porta alla
espressione:
![$\displaystyle {\cal L} = {1\over 4}F^{\mu\nu} F_{\mu\nu} + j^\mu A_\mu + {c\over 2}[(\partial_\mu A^\mu)^2 - \partial_\mu A^\nu \partial_\nu A^\mu]$](img1882.png) |
(5.27) |
adesso però si può vedere subito facendo i conti che:
quindi il termine indeterminato in 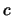 è una quadridivergenza e pertanto può
essere anche eliminato essendo inessenziale, resta così l'espressione finale:
è una quadridivergenza e pertanto può
essere anche eliminato essendo inessenziale, resta così l'espressione finale:
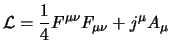 |
(5.28) |
Un modo diverso di ottenere questo risultato è quello di partire dalle
equazioni del moto scritte come:
ed ottenere un principio di minima azione che ci permetta di identificare una
lagrangiana moltiplicando queste per una variazione infinitesima dei campi
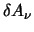 (che sia nulla agli estremi) ed integrando sul quadrivolume
compreso fra due ipersuperfici
(che sia nulla agli estremi) ed integrando sul quadrivolume
compreso fra due ipersuperfici 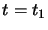 e
e  ottenendo che:
(dove si è integrato per parti il primo addendo sfruttando l'annullarsi di
ottenendo che:
(dove si è integrato per parti il primo addendo sfruttando l'annullarsi di
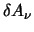 agli estremi); adesso per il secondo addendo è immediato
considerare che:
dato che
agli estremi); adesso per il secondo addendo è immediato
considerare che:
dato che 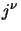 non dipende dai campi; per il primo termine invece
consideriamo che
non dipende dai campi; per il primo termine invece
consideriamo che
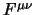 è antisimmetrico, pertanto nella contrazione con
è antisimmetrico, pertanto nella contrazione con
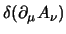 si ha che il pezzo dovuto alla parte simmetrica di questo
termine è identicamente nullo, dunque la sola parte significativa del prodotto
è quella con la parte antisimmetrica e si ha che:
adesso una immediata generalizzazione della formula
si ha che il pezzo dovuto alla parte simmetrica di questo
termine è identicamente nullo, dunque la sola parte significativa del prodotto
è quella con la parte antisimmetrica e si ha che:
adesso una immediata generalizzazione della formula
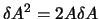 ci
dice che:
(basta applicarla termine a termine) dunque alla fine si ha:
e allora è immediata l'identificazione:
che è quello che volevamo dimostrare.
ci
dice che:
(basta applicarla termine a termine) dunque alla fine si ha:
e allora è immediata l'identificazione:
che è quello che volevamo dimostrare.
Si noti che in presenza di una corrente esterna questa lagrangiana non è
invariante per trasformazioni di gauge, però il termine aggiuntivo che
otteniamo è nella forma:
dove il passaggio è giustificato dato che per l'equazione di continuità
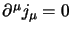 ; questo ci porta all'invarianza delle equazioni di Maxwell, ma
ci dice anche che la conservazione della carica è condizione necessaria e
sufficiente per l'invarianza di gauge della teoria.
; questo ci porta all'invarianza delle equazioni di Maxwell, ma
ci dice anche che la conservazione della carica è condizione necessaria e
sufficiente per l'invarianza di gauge della teoria.
Per la sua importanza nel caso quantistico possiamo partire anche da un altro
punto di vista, restringendo l'arbitrarietà di 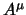 ; la scelta più ovvia per
mantenere il formalismo covariante è la gauge di Lorentz:
; la scelta più ovvia per
mantenere il formalismo covariante è la gauge di Lorentz:
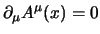 |
(5.29) |
che riduce la (4.24) a:
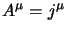 |
(5.30) |
e dove l'arbitrarietà di 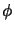 per trasformazioni di gauge è ridotta ai soli
per trasformazioni di gauge è ridotta ai soli
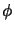 che soddisfino l'equazione delle onde:
che soddisfino l'equazione delle onde:
Il procedimento ci dice cioè che scelta una lagrangiana nella forma
(4.28) la conservazione della carica implica
l'invarianza di gauge e viceversa; dal principio di minima azione si ottengono
poi le equazioni di Maxwell.
Si può però fare una trattazione alternativa in cui la gauge di Lorentz può
essere incorporata nella teoria: infatti se aggiungiamo un termine
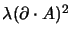 alla lagrangiana (4.28)
questo porta nelle equazioni del moto(4.24) un termine
ulteriore:
alla lagrangiana (4.28)
questo porta nelle equazioni del moto(4.24) un termine
ulteriore:
(si è utilizzata la (4.25)
per il passaggio intermedio) che così diventerebbero:
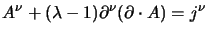 |
(5.31) |
adesso qui prendiamo la divergenza di ambo i membri ed usiamo al solito
l'equazione di continuità; si ottiene che:
per cui se
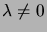 si può concludere che:
si può concludere che:
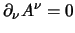 |
(5.32) |
e basta che
 vada a zero per
vada a zero per
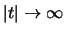 per avere
per avere
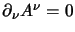 a tutti i tempi, si è cioè ottenuta la condizione di
Lorentz, che sostituita nella (4.31) ci dà le
equazioni delle onde.
a tutti i tempi, si è cioè ottenuta la condizione di
Lorentz, che sostituita nella (4.31) ci dà le
equazioni delle onde.
In questo caso si parte dalla scelta della lagrangiana e dalla conservazione
della carica: il principio di minima azione implica la
(4.32), mentre le condizioni al contorno implicano la
gauge di Lorentz e le equazioni di Maxwell nella forma di equazioni di
D'Alambert per i potenziali.





Next: Il campo di Klein-Gordon.
Up: I campi classici.
Previous: I campi classici.
Contents
Index
Simone Piccardi
2003-02-20
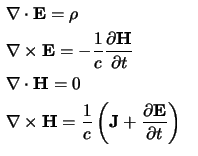
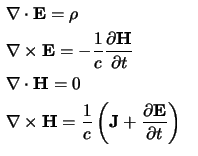

![]() . Come già detto queste equazioni
covarianti esprimono l'invarianza relativistica delle leggi
dell'elettromagnetismo: due importanti invarianti connessi col campo
elettromagnetico, che si ottengono immediatamente dalle contrazioni del
tensore elettromagnetico, sono allora:
. Come già detto queste equazioni
covarianti esprimono l'invarianza relativistica delle leggi
dell'elettromagnetismo: due importanti invarianti connessi col campo
elettromagnetico, che si ottengono immediatamente dalle contrazioni del
tensore elettromagnetico, sono allora:
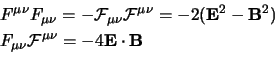
![]() e
e
![]() , ma le
equazioni di Maxwell, che dovremmo riottenere dalla teoria, sono del primo
ordine, mentre le equazioni di Eulero del §4.2 sono del
secondo ordine, inoltre in un tal modo otterremmo anche grosse difficoltà a
far emergere in modo naturale la covarianza del procedimento.
, ma le
equazioni di Maxwell, che dovremmo riottenere dalla teoria, sono del primo
ordine, mentre le equazioni di Eulero del §4.2 sono del
secondo ordine, inoltre in un tal modo otterremmo anche grosse difficoltà a
far emergere in modo naturale la covarianza del procedimento.
![]() col quale si
possono trasformare le equazioni di Maxwell del primo ordine in un insieme di
equazioni equivalenti del secondo ordine; abbiamo già visto che i campi si
possono esprimere nella forma:
col quale si
possono trasformare le equazioni di Maxwell del primo ordine in un insieme di
equazioni equivalenti del secondo ordine; abbiamo già visto che i campi si
possono esprimere nella forma:

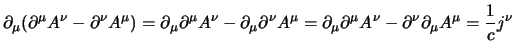
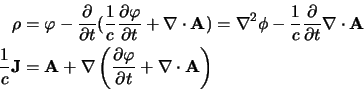
![]() ); essa
permette di eliminare ogni derivata rispetto al tempo dalla prima di queste
due equazioni, che diventa così un vincolo indipendente dal tempo, e permette
di determinare il potenziale come:
); essa
permette di eliminare ogni derivata rispetto al tempo dalla prima di queste
due equazioni, che diventa così un vincolo indipendente dal tempo, e permette
di determinare il potenziale come:
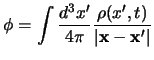
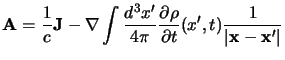
![]() . Questa
ha il grande pregio di mantenere manifesta la covarianza della teoria e di
semplificare le (4.24), dando luogo a delle equazioni (le
equazioni delle onde trovate al §1.4)
identiche per tutte le componenti dei potenziali; essa però, come vedremo in
seguito, non rimuove completamente l'arbitrarietà dei potenziali.
. Questa
ha il grande pregio di mantenere manifesta la covarianza della teoria e di
semplificare le (4.24), dando luogo a delle equazioni (le
equazioni delle onde trovate al §1.4)
identiche per tutte le componenti dei potenziali; essa però, come vedremo in
seguito, non rimuove completamente l'arbitrarietà dei potenziali.
![]() . Questo però comporta un
problema; sappiamo infatti che i potenziali non sono delle quantità
osservabili direttamente, dato che dipendono dalla scelta della gauge; questo
causerà delle difficoltà nella quantizzazione perché essi non possono essere
considerati come variabili dinamiche indipendenti; per ora comunque ci
limiteremo a cercare un'espressione per la densità di lagrangiana
. Questo però comporta un
problema; sappiamo infatti che i potenziali non sono delle quantità
osservabili direttamente, dato che dipendono dalla scelta della gauge; questo
causerà delle difficoltà nella quantizzazione perché essi non possono essere
considerati come variabili dinamiche indipendenti; per ora comunque ci
limiteremo a cercare un'espressione per la densità di lagrangiana ![]() del
campo elettromagnetico con la quale poi esprimere anche le altre quantità
misurabili.
del
campo elettromagnetico con la quale poi esprimere anche le altre quantità
misurabili.
![]() partiamo dal fatto che sappiamo che il quadripotenziale
partiamo dal fatto che sappiamo che il quadripotenziale
![]() è un quadrivettore, mentre ci occorre uno scalare invariante funzione
di esso e delle sue derivate prime. L'invarianza di gauge delle equazioni del
moto non comporta automaticamente anche quella della lagrangiana; sappiamo
infatti che tutte le possibili scelte di una lagrangiana a meno della
quadridivergenza di una funzione qualunque danno luogo alle stesse equazioni
del moto, per cui dall'invarianza di gauge otteniamo solo l'ulteriore
richiesta che per trasformazioni di gauge dei potenziali la lagrangiana debba
avere al più una divergenza aggiuntiva.
è un quadrivettore, mentre ci occorre uno scalare invariante funzione
di esso e delle sue derivate prime. L'invarianza di gauge delle equazioni del
moto non comporta automaticamente anche quella della lagrangiana; sappiamo
infatti che tutte le possibili scelte di una lagrangiana a meno della
quadridivergenza di una funzione qualunque danno luogo alle stesse equazioni
del moto, per cui dall'invarianza di gauge otteniamo solo l'ulteriore
richiesta che per trasformazioni di gauge dei potenziali la lagrangiana debba
avere al più una divergenza aggiuntiva.
![]() ):
):
![]() ) usando la relazione base
) usando la relazione base
![]() ; il primo termine da esaminare è:
; il primo termine da esaminare è:
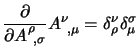
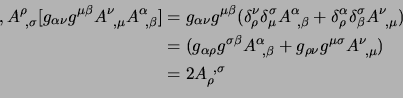
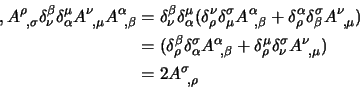
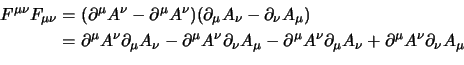
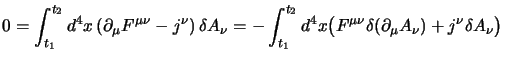
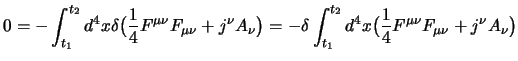
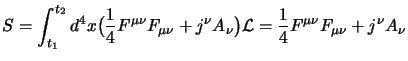
![]() ; la scelta più ovvia per
mantenere il formalismo covariante è la gauge di Lorentz:
; la scelta più ovvia per
mantenere il formalismo covariante è la gauge di Lorentz:
![]() alla lagrangiana (4.28)
questo porta nelle equazioni del moto(4.24) un termine
ulteriore:
alla lagrangiana (4.28)
questo porta nelle equazioni del moto(4.24) un termine
ulteriore: