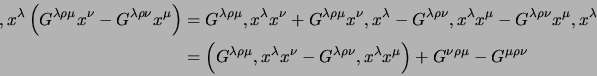



Next: I campi classici.
Up: La meccanica analitica dei
Previous: L'invarianza di gauge di
Contents
Index
Il teorema di Belinfante.
E' importante notare che il tensore energia-impulso, dipendendo anche dalla
lagrangiana che è sempre definita a meno di una quadridivergenza, non è
definito univocamente. Dato che ciò che deve essere univoco sono le
osservabili fisiche (come l'energia e l'impulso) è immediato osservare che
data la definizione (4.15) si possono ricavare altri infiniti
tensori energia-impulso, tutti equivalenti, nella forma:
dove
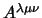 è un tensore qualsiasi che soddisfi alla condizione:
che sia cioè antisimmetrico rispetto ai primi due indici e che si annulli
all'infinito (cioè per
è un tensore qualsiasi che soddisfi alla condizione:
che sia cioè antisimmetrico rispetto ai primi due indici e che si annulli
all'infinito (cioè per
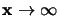 ).
).
Per dimostrare l'equivalenza notiamo che per la simmetria delle
derivate parziali
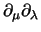 e l'antisimmetria di
e l'antisimmetria di
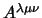 appena vista si ha immediatamente:
appena vista si ha immediatamente:
dato che è banalmente
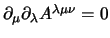 . Ovviamente
questo non basta per l'equivalenza di
. Ovviamente
questo non basta per l'equivalenza di
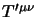 e
e
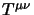 , occorre che
sia lo stesso anche il quadrimpulso
, occorre che
sia lo stesso anche il quadrimpulso 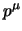 , che abbiamo visto essere:
adesso però la somma
, che abbiamo visto essere:
adesso però la somma
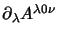 per l'antisimmetria si
riduce a
per l'antisimmetria si
riduce a
 e ottengo così l'integrale tridimensionale di
una divergenza che tratto col teorema di Gauss, andando sulla superficie
all'infinito dove
e ottengo così l'integrale tridimensionale di
una divergenza che tratto col teorema di Gauss, andando sulla superficie
all'infinito dove
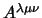 è nullo per cui questo termine se ne va;
resta così solo l'integrale di
è nullo per cui questo termine se ne va;
resta così solo l'integrale di
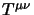 per cui alla fine
per cui alla fine
 .
.
Un ragionamento del tutto analogo si può fare col tensore densità di momento
angolare
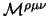 sfruttando un qualsiasi tensore
sfruttando un qualsiasi tensore
 antisimmetrico rispetto ai primi due indici e che
vada a zero per x che va all'infinito; in tal caso con lo stesso identico
procedimento di prima si otterrà che:
antisimmetrico rispetto ai primi due indici e che
vada a zero per x che va all'infinito; in tal caso con lo stesso identico
procedimento di prima si otterrà che:
è perfettamente equivalente a
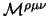 .
.
Date queste relazioni possiamo dimostrare il teorema di Belinfante,
che premette di scrivere
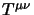 e
e
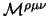 in forma
semplificata.
in forma
semplificata.
Il punto di partenza è la considerazione che l'espressione
(4.15) del tensore energia-impulso ci mostra che non è detto
che
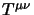 sia simmetrico, per cui in generale occorre stare molto
attenti rispetto all'indice su cui si deriva per ottenere la conservazione del
quadrimpulso.
sia simmetrico, per cui in generale occorre stare molto
attenti rispetto all'indice su cui si deriva per ottenere la conservazione del
quadrimpulso.
Questa condizione si può ricavare direttamente dalle leggi di conservazione di
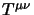 e
e
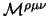 con l'espressione
(4.19) di quest'ultimo, se infatti poniamo:
con l'espressione
(4.19) di quest'ultimo, se infatti poniamo:
usando la conservazione di
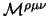 e la
(4.19) otterremo che:
adesso qui possiamo svolgere i conti sul primo addendo ed usando la legge di
conservazione per
e la
(4.19) otterremo che:
adesso qui possiamo svolgere i conti sul primo addendo ed usando la legge di
conservazione per
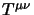 sarà:
da cui segue immediatamente:
sarà:
da cui segue immediatamente:
 |
(5.20) |
quindi
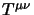 non è simmetrico, a meno che non sia nullo
non è simmetrico, a meno che non sia nullo
 , cosa che avviene solo (visto che questo è il termine dovuto
allo spin) solo per campi scalari.
, cosa che avviene solo (visto che questo è il termine dovuto
allo spin) solo per campi scalari.
Il teorema di Belinfante però ci assicura che è sempre possibile ottenere un
tensore energia impulso equivalente che sia simmetrico. Per farlo definiamo
il tensore:
 |
(5.21) |
e verifichiamo che il tensore:
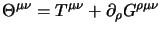 |
(5.22) |
è equivalente a
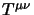 .
.
Per farlo sfruttiamo quanto visto prima, anzitutto mostriamo che
 è antisimmetrico nei primi due indici. Per farlo usiamo le
definizione (4.21); si avrà che:
è antisimmetrico nei primi due indici. Per farlo usiamo le
definizione (4.21); si avrà che:
adesso però sappiamo
 è antisimmetrico negli ultimi due indici
(per le proprietà delle
è antisimmetrico negli ultimi due indici
(per le proprietà delle
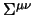 ) per cui si avrà:
e confrontando questa con la definizione (4.21) si
ha la definitiva:
quindi l'antisimmetria è dimostrata, l'altra condizione poi è immediatamente
soddisfatta in quanto
) per cui si avrà:
e confrontando questa con la definizione (4.21) si
ha la definitiva:
quindi l'antisimmetria è dimostrata, l'altra condizione poi è immediatamente
soddisfatta in quanto
 è una combinazione lineare dei campi e
pertanto dato che si annullano all'infinito lo fa pure lui.
è una combinazione lineare dei campi e
pertanto dato che si annullano all'infinito lo fa pure lui.
Adesso quello che si deve far vedere è che
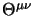 è simmetrico,
dalla (4.22) abbiamo subito che:
è simmetrico,
dalla (4.22) abbiamo subito che:
ma per la (4.20) questa diventa:
e basta usare la definizione per
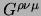 e sviluppare il conto
per ottenere:
adesso qui consideriamo che
e sviluppare il conto
per ottenere:
adesso qui consideriamo che
 quindi si può
semplificare ottenendo:
e se confrontiamo con la (4.21) si vede subito che
questa è:
dunque
quindi si può
semplificare ottenendo:
e se confrontiamo con la (4.21) si vede subito che
questa è:
dunque
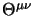 è simmetrico; per questa proprietà
è simmetrico; per questa proprietà
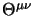 è
chiamato tensore energia-impulso canonico.
è
chiamato tensore energia-impulso canonico.
Con
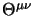 si può anche semplificare l'espressione della densità di
momento angolare; se sostituiamo nella definizione a
si può anche semplificare l'espressione della densità di
momento angolare; se sostituiamo nella definizione a
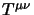 infatti si
ha:
infatti si
ha:
vale a dire, svolgendo i conti:
per valutare la parentesi quadra consideriamo che:
adesso consideriamo gli ultimi due addendi scrivendoceli esplicitamente; si ha:
e qui basta invertire gli ultimi due indici del secondo per avere che:
dunque si ottiene che:
quindi si può scrivere il tensore densità di momento angolare come:
e allora dato che evidentemente il termine in parentesi è antisimmetrico nei
primi due indici (lo è
 ) e si annulla all'infinito (ci
pensano i campi dentro
) e si annulla all'infinito (ci
pensano i campi dentro
 ) questo è un tensore perfettamente
equivalente a:
che può essere usato come forma semplificata della densità di momento
angolare.
) questo è un tensore perfettamente
equivalente a:
che può essere usato come forma semplificata della densità di momento
angolare.




Next: I campi classici.
Up: La meccanica analitica dei
Previous: L'invarianza di gauge di
Contents
Index
Simone Piccardi
2003-02-20
![]() e l'antisimmetria di
e l'antisimmetria di
![]() appena vista si ha immediatamente:
appena vista si ha immediatamente:
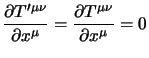
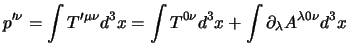
![]() sfruttando un qualsiasi tensore
sfruttando un qualsiasi tensore
![]() antisimmetrico rispetto ai primi due indici e che
vada a zero per x che va all'infinito; in tal caso con lo stesso identico
procedimento di prima si otterrà che:
antisimmetrico rispetto ai primi due indici e che
vada a zero per x che va all'infinito; in tal caso con lo stesso identico
procedimento di prima si otterrà che:
![]() e
e
![]() in forma
semplificata.
in forma
semplificata.
![]() sia simmetrico, per cui in generale occorre stare molto
attenti rispetto all'indice su cui si deriva per ottenere la conservazione del
quadrimpulso.
sia simmetrico, per cui in generale occorre stare molto
attenti rispetto all'indice su cui si deriva per ottenere la conservazione del
quadrimpulso.
![]() e
e
![]() con l'espressione
(4.19) di quest'ultimo, se infatti poniamo:
con l'espressione
(4.19) di quest'ultimo, se infatti poniamo:
![]() è antisimmetrico nei primi due indici. Per farlo usiamo le
definizione (4.21); si avrà che:
è antisimmetrico nei primi due indici. Per farlo usiamo le
definizione (4.21); si avrà che:
![]() è simmetrico,
dalla (4.22) abbiamo subito che:
è simmetrico,
dalla (4.22) abbiamo subito che:
![]() si può anche semplificare l'espressione della densità di
momento angolare; se sostituiamo nella definizione a
si può anche semplificare l'espressione della densità di
momento angolare; se sostituiamo nella definizione a
![]() infatti si
ha:
infatti si
ha: