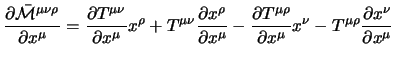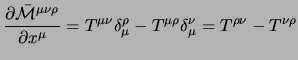L'invarianza per traslazioni e rotazioni.

Un caso particolare di invarianza che ci deve essere per tutti i sistemi relativistici è quella per le traslazioni spazio-temporali e per le trasformazioni di Lorentz; vediamo allora cosa comporta per esse il teorema della Noeter.

Cominciamo con le traslazioni spazio-temporali, in questo caso una trasformazione infinitesima delle coordinate si può sempre scrivere nella forma:

$$x'_\mu = x_\mu + \epsilon_\mu$$

se questa però vogliamo usarla per sfruttare quanto visto usando la forma generica delle trasformazioni vista nelle (4.17) dovremo riscriverla in una forma più opportuna come:

$$x'_\mu = x_\mu + g_\mu^\nu \epsilon_\nu \ee \delta x_\mu = g_\mu^\nu \epsilon_\nu$$

e questa ci mostra come in questo caso l'indice $n$ diventi un indice covariante $\nu$ e come in questo caso sia $X^n_\mu = X^\nu_\mu = g^\nu_\mu$, i campi invece sono comunque invarianti per traslazione per cui $\delta\phi = 0$ ed evidentemente $Y_i^n = Y_i^\nu = 0$ dunque dalla (4.18) si ha immediatamente:

$${\partial{}\over \partial x^\mu} \left[ T^{\mu\nu} g_{\nu}^\rho \right] = 0 \ssp{cioè} \partial_\mu T^{\mu\nu}=0$$

Per le trasformazioni di Lorentz le cose sono un po' più complesse, infatti se vogliamo mantenere le notazioni tensoriali che ci danno le proprietà di tensoriali dei sei angoli covarianti $\omega_{\alpha\beta}$ che sono i parametri indipendenti delle trasformazioni, bisogna stare molto attenti alla proprietà di antisimmetria $\omega_{\alpha\beta}=-\omega_{\beta\alpha}$ ed al fatto che quando si fa la semplificazione dei parametri che porta alla (4.18) occorre semplificare su relazioni indipendenti, ed una relazione del tipo $A^{\alpha\beta} \omega_{\alpha\beta}=0$ non comporta più $A^{\alpha\beta}=0$ dato che la parte simmetrica di quest'ultimo nel prodotto è nulla in ogni caso.

Al solito allora potremo effettuare la semplificazione ed ottenere relazioni indipendenti soltanto con quantità antisimmetriche negli indici. Nel §2.3.2 abbiamo visto che le trasformazioni infinitesime sono date dalla (2.28) per cui le coordinate si possono esprimere come:

$$x'_\mu = x_\mu +\omega_{\mu\sigma}x^\sigma$$

per cui sarà:

$$\delta x_\mu = \omega_{\rho\sigma} g_\mu^\rho x^\sigma$$

ma qui non ho una quantità antisimmetrica a moltiplicare $\omega_{\rho\sigma}$ per cui si deve antisimmetrizzare questa come:

$$\delta x_\mu = \half \omega_{\rho\sigma} \left( g_\mu^\rho x^\sigma - g_\mu^\sigma x^\rho \right) = \omega_{\rho\sigma} X^{\rho\sigma}_\mu$$

e questa ha tutti i coefficienti indipendenti per cui possiamo inserire nella (4.18) il termine:

$$X^{\rho\sigma}_\mu = \half \left( g_\mu^\rho x^\sigma - g_\mu^\sigma x^\rho \right)$$

dove al posto di $n$ si hanno gli indici $\rho$ e $\sigma$.

Per i campi le cose sono più complesse dato che il loro comportamento dipende da cosa il campo rappresenta; se il campo è scalare ovviamente sarà invariante e gli $Y$ saranno nulli; ma si possono avere campi vettoriali, tensoriali ecc. nel qual caso le trasformazioni di Lorentz mescoleranno opportunamente le varie componenti. In genere i campi che si usano sono o campi spinoriali di spin 1/2 come il campo di Dirac o campi vettoriali come il campo elettromagnetico; in questi casi i generatori $G_{ij}$ sono matrici nello spazio vettoriale dei campi e allora si usa scrivere in componenti che:

$$\delta \phi_i = \half \omega_{\rho\sigma} \Sigma^{\rho\sigma}_{ij} \phi_j = \omega_{\rho\sigma} Y^{\rho\sigma}_i$$

dove le $\Sigma^{\mu\nu}_{ij}$ (antisimmetriche in $\mu$ e $\nu$) fanno le veci di quelle che per le rotazioni normali sono le matrici $\sigma$ di Pauli (ed è questa la ragione del fattore 1/2); da questa si ottiene:

$$Y^{\rho\sigma}_i = \half \Sigma^{\rho\sigma}_{ij} \phi_j$$

nel caso del campo di Dirac poi conosciamo già le $\Sigma^{\mu\nu}_{ij}$ e abbiamo visto che sono le matrici $\sigma^{\mu\nu}$ incontrate al §2.3.2 ed espresse dalla (2.33).

Adesso per trovare le quantità conservate associate alle trasformazioni di Lorentz possiamo sostituire le espressioni trovate per $X$ e $Y$ nella (4.18) ottenendo:

$${\partial{}\over \partial x^\mu} \left[ \half \left( - \pi_i^\m... ...left( g_\nu^\rho x^\sigma - g_\nu^\sigma x^\rho \right) \right) \right] = 0$$

e se definiamo il tensore densità di momento angolare:

$${\cal M}^{\mu\rho\sigma} = T^{\mu\rho} x^\sigma - T^{\mu\sigma} x^\rho - \pi_i^\mu \Sigma^{\rho\sigma}_{ij} \phi_j$$ (5.19)

(antisimmetrico in $\rho$ e $\sigma$) la precedente diventa:

$${\partial{{\cal M}^{\mu\rho\sigma}}\over \partial x^\mu} = 0$$

ed in generale se i campi sono qualcosa di più complesso dovremo lasciare l'ultimo termine della (4.19) in forma implicita come $\pi_i^\mu Y^{\rho\sigma}_i$.

Viste queste relazioni si possono studiare le quantità conservate, dal tensore energia-impulso si ottengono le costanti del moto relative all'invarianza per traslazione del sistema, che sono dunque le componenti del quadrimpulso dei campi date da:

$$p^\mu=\int d^3x T^{0\mu}$$

dal tensore densità di momento angolare si ottengono invece le costanti del moto derivanti dall'invarianza di rotazione che sono le sei componenti del tensore di momento angolare definite dalla relazione:

$$M^{\mu\nu}=\int d^3x {\cal M}^{0\mu\nu}$$

(che evidentemente è un tensore antisimmetrico per le proprietà degli ultimi due indici del tensore densità di momento angolare).

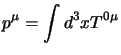
Un modo alternativo di dimostrare la conservazione del quadrimpulso si può ottenere sfruttando direttamente le equazioni del moto; dalla definizione del tensore energia-impulso si ha che:

$${\partial{T^{\mu\nu}}\over \partial x^\mu} = {\partial{}\over \p... ... x^\mu} \pd{\phi},{x_\nu} - {\partial{\cal L}\over \partial x^\mu} g^{\mu\nu}$$

adesso possiamo usare le equazioni del moto per il primo di questi tre addendi ottenendo:

$${\partial{T^{\mu\nu}}\over \partial x^\mu} = \pd{\cal L},{\phi} \... ...pd{\cal L},{\phi_\mu} \pd{^2\phi},{x^\mu\partial x_\nu} - \pd{\cal L},{x_\nu}$$

(si è anche esplicitata la derivata nel secondo e sistemato l'indice nel terzo); adesso però se ${\cal L}$ non dipende da $x$ (cosa sempre vera quando c'è invarianza per traslazione), avremo che:

$$\pd{\cal L},{x_\nu} = \pd{\cal L},{\phi} \phi^\nu + \pd{\cal L},{\phi_\mu} \pd{\phi_\mu},{x_\nu}$$

che sostituito nella precedente ci da immediatamente:

$${\partial{T^{\mu\nu}}\over \partial x^\mu} = \pd{\cal L},{\phi_\... ... \pd{^2\phi},{x^\mu\partial x_\nu} - \pd{^2\phi},{x_\nu\partial x^\mu} \right)$$

e la regolarità dei campi ci assicura che, per il teorema di Schwartz, anche la parentesi tonda è nulla per cui si ottiene la conservazione del quadrimpulso.

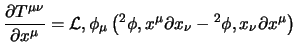
Per il momento angolare le cose sono ovviamente più complesse; ovviamente è sempre naturale definirlo come

$$\bar{\cal M}^{\mu\nu\rho} = T^{\mu\nu}x^\rho - T^{\mu\rho}x^\nu$$

da cui derivando:

$${\partial{\bar{\cal M}^{\mu\nu\rho}}\over \partial x^\mu} = {\par... ...over \partial x^\mu} x^\nu - T^{\mu\rho} {\partial{x^\nu}\over \partial x^\mu}$$

adesso qui $\partial_\mu T^{\mu\nu} = \partial_\mu T^{\mu\rho}=0$ per cui con pochi conti si ottiene che:

$${\partial{\bar{\cal M}^{\mu\nu\rho}}\over \partial x^\mu} = T^{\mu\nu} \delta_\mu^\rho - T^{\mu\rho} \delta_\mu^\nu = T^{\rho\nu} - T^{\nu\rho}$$

dunque, a meno che $T^{\mu\nu}$ non sia simmetrico $\bar{\cal M}^{\mu\nu\rho}$ non ci da una quantità conservata; il che è logico dato che questo è solo il momento angolare orbitale, e ci manca lo spin trasportato dal campo stesso.