Alcuni concetti base

In meccanica quantistica lo stato di un sistema è rappresentato da un vettore di stato normalizzato $\ket{\psi}$ in un opportuno spazio di Hilbert, oppure, nel caso generale di miscela di stati, da una matrice densità $\rho=\sum_i p_i\ket{\psi_i}\bra{\psi_i}$. Le quantità osservabili sono associate a operatori hermitiani (o autoaggiunti) $\op A =\op A^\dagger$ e il valor medio di una misura di una osservabile $\op{A}$ su un sistema nello stato $\ket{\psi}$ è dato da $\bra{\psi}\op{A}\ket{\psi}$.

Le osservabili si ottengono col principio di corrispondenza; si tratta cioè di sostituire alle quantità numeriche delle relazioni classiche della meccanica analitica gli opportuni operatori; individuate le coordinate lagrangiane $q_i$ del sistema ed i rispettivi momenti coniugati $p_i$ come osservabili di base il principio fornisce i corrispondenti operatori quantistici tramite le relazioni:

$$[\op{q}_i,\op{p}_j]=i\hbar \delta_{ij}$$

così ad esempio otteniamo, per una particella libera, che l'operatore associato all'osservabile impulso è ${\bf p}\to -i\hbar \nabla$.

L'evoluzione dinamica del sistema è data poi dall'equazione di Schroedinger:

$$i\hbar {\partial{\ket{\psi(t)}}\over \partial t}= \op{H}\ket{\psi(t)}$$ (3.1)

dove $\op{H}=\op{H}^\dagger$ è l'operatore associato all'hamiltoniana del sistema, ottenuto col principio di corrispondenza dalla espressione della meccanica analitica in termini delle variabili canoniche. Ovviamente questa è un osservabile (l'energia) e quindi autoaggiunto.

In modo equivalente si può usare la rappresentazione di Heisemberg, in tal caso dato lo stato ad un istante iniziale $\ket{\psi_0}=\ket{\psi(t_0)}$ si avrà:

$$\ket{\psi(t)}= \op{U}(t;t_0)\ket{\psi(t_0)}$$

dove $\op{U}(t;t_0)$ è un operatore unitario (cioè $\op{U}^\dagger =\op{U}^{-1}$) detto operatore di evoluzione che, come si può ottenere dalla (2.1), obbedisce all'equazione di Heisemberg:

$$i\hbar {\partial{\op{U}(t,t_0)}\over \partial t}=\op H(t) \op{U}(t,t_0)$$ (3.2)

L'equazione di Schroedinger comunque gioca un ruolo fondamentale; infatti è a partire dal principio di corrispondenza che si riesce a costruire l'hamiltoniana e poi quest'equazione; le altre si ottengono poi attraverso cambiamenti di rappresentazione nello spazio di Hilbert, per cui quando vorremo costruire una meccanica quantistica relativistica dovremo comunque partire da essa.

Quando si cerca di estendere tutto questo alla relatività ristretta ci si trova di fronte ad una difficoltà; infatti in relatività il tempo e lo spazio non possono essere trattati separatamente e nel caso di una particella singola si ottiene l'espressione (1.50) per energia ed impulso vista in §1.3.1, che ci dice la possibilità di un'equivalenza massa-energia.

Il problema nasce allora proprio qui. Quando si va a cercare una descrizione relativistica di una particella puntiforme troviamo sempre una scala fondamentale per l'impulso che è $p=mc$ e quindi una lunghezza d'onda Compton:

$$\lambda={h\over mc}$$

allora dato che per il principio di indeterminazione si ha che $\Delta x\Delta p \sim \hbar$ per individuare una particella su distanze inferiori a $\lambda$ otteniamo un'incertezza sul momento dell'ordine di $mc$, cioè sufficiente alla creazione di nuove particelle, viene così a perdere senso il concetto di particella singola.

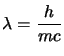
Questo ci dice subito che la meccanica quantistica relativistica avrà senso in questo intervallo di energie intermedio, andando oltre diventerà necessario ricorrere alla teoria dei campi.