| (2.42) |
Inoltre ci interessa ottenere la conservazione dell'energia e della quantità di moto che sono leggi generali che devono restare valide anche in relatività ristretta; per farlo cominciamo col definire come quadrimpulso il quadrivettore:
Adesso si tratta di capire quali sono le caratteristiche di ![]() , e dato
che vogliamo ottenere la conservazione della quantità di moto (che è una legge
che deve essere valida in tutti i sistemi di riferimento) la conservazione di
tale quadrivettore sarebbe l'ideale; vedremo poi che essa comporta, al limite
di
, e dato
che vogliamo ottenere la conservazione della quantità di moto (che è una legge
che deve essere valida in tutti i sistemi di riferimento) la conservazione di
tale quadrivettore sarebbe l'ideale; vedremo poi che essa comporta, al limite
di ![]() , anche la conservazione dell'energia cinetica classica.
, anche la conservazione dell'energia cinetica classica.
Se come legge di conservazione imponiamo che sia
![]() questo significa che tutte le componenti del quadrivettore si conservano;
allora per le componenti spaziali quello che si conserva è:
questo significa che tutte le componenti del quadrivettore si conservano;
allora per le componenti spaziali quello che si conserva è:
Abbiamo visto cosa sono le componenti spaziali del quadrimpulso, che possiamo
identificare con una quantità di moto; diventa così logico usare per la forza
in tre dimensioni
![]() la definizione riportata in
(1.41) che resterà valida in tutti i sistemi
inerziali, anche se in generale
la definizione riportata in
(1.41) che resterà valida in tutti i sistemi
inerziali, anche se in generale
![]() sarà diversa al cambiare del
sistema di riferimento e non potrà essere identificata con la parte spaziale
di un quadrivettore.
sarà diversa al cambiare del
sistema di riferimento e non potrà essere identificata con la parte spaziale
di un quadrivettore.
Resta da interpretare la componente temporale ![]() , ed inoltre dobbiamo
chiarire la relazione fra il quadrimpulso e la forza espressa con la
(1.43), pertanto proviamo a calcolare la
rerivata:
, ed inoltre dobbiamo
chiarire la relazione fra il quadrimpulso e la forza espressa con la
(1.43), pertanto proviamo a calcolare la
rerivata:
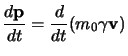
![$\displaystyle {\bf v}\cdot{d{\bf p}\over dt}=m_0 \left[ v^2{d{\gamma}\over dt}+\gamma
{\bf v}\cdot{d{\bf v}\over dt}\right]
$](img214.png)
![$\displaystyle {\bf v}\cdot{d{\bf p}\over dt}
= m_0 \left[{v^2\over c^2-v^2}\ga...
...ht]
= m_0\gamma {\bf v}\cdot{d{\bf v}\over dt} \left[{c^2\over c^2-v^2}\right]
$](img215.png)
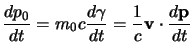
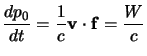
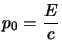
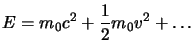
Infine ritorniamo all'espressione esplicita per la forza di Minkowsky definita in (1.43), che per quanto trovato sopra può essere scritta come:
Si noti che in realtà qui ci si è limitati a esprimere la conservazione dell'energia e della quantità di moto tramite la conservazione del quadrimpulso, facendo vedere come da questa al limite classico si riottengano le precedenti, in modo da avere, con un'analogia, le espressioni per l'energia e l'impulso relativistiche; abbiamo così ottenuto le formule giuste. Non abbiamo però dimostrato effettivamente che sono necessariamente queste.
In realtà le espressioni relativistiche dell'energia e della quantità di moto
si possono ottenere rigorosamente in altri modi; uno di questi, molto formale,
utilizza di un impianto analogo a quello della meccanica analitica, costruendo
una lagrangiana da cui derivare le equazioni del moto tramite il principio di
minima azione; un altro ricorre invece ai due principi fondamentali della
conservazione dell'energia e dell'impulso dai quali (per il procedimento vedi
[Jac]) si possono ricavare dette espressioni in via del tutto
generale con argomenti di carattere teorico, (basandosi sui postulati ed
usando considerazioni sull'urto elastico di due particelle identiche),
imponendo la condizione che esse si riducano alle usuali per ![]() .
.
Infine è di notevole interesse il modulo del quadrimpulso, da quanto ottenuto sappiamo che possiamo esprimere quest'ultimo come:
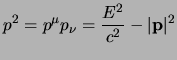
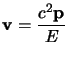
Il quadrimpulso ![]() ci dà una descrizione completa della cinematica di una
particella; quindi l'assegnazione della massa di una particella e della sua
velocità v (o dell'impulso p) in un qualsiasi sistema di
riferimento ci permette di determinarne le proprietà cinematiche; negli
esperimenti con acceleratori però diventa più conveniente usare come variabili
cinematiche le due componenti di p perpendicolari all'asse
ci dà una descrizione completa della cinematica di una
particella; quindi l'assegnazione della massa di una particella e della sua
velocità v (o dell'impulso p) in un qualsiasi sistema di
riferimento ci permette di determinarne le proprietà cinematiche; negli
esperimenti con acceleratori però diventa più conveniente usare come variabili
cinematiche le due componenti di p perpendicolari all'asse ![]() (preso
lungo la direzione del fascio) che indicheremo con
(preso
lungo la direzione del fascio) che indicheremo con
![]() e la
rapidità
e la
rapidità ![]() definita dalle (1.7).
definita dalle (1.7).
Se in un riferimento ![]() una particella ha impulso p con impulso
trasversale
una particella ha impulso p con impulso
trasversale
![]() e una componente lungo
e una componente lungo ![]() pari a
pari a ![]() esiste una
unica trasformazione di Lorentz lungo l'asse
esiste una
unica trasformazione di Lorentz lungo l'asse ![]() che porta ad un
riferimento
che porta ad un
riferimento ![]() in cui
in cui ![]() è nulla. Allora in
è nulla. Allora in ![]() l'impulso e l'energia
della particella saranno:
l'impulso e l'energia
della particella saranno:
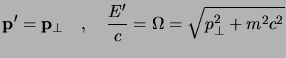
Nota poi la rapidità ![]() di questa trasformazione, partendo dalle
precedenti componenti del quadrimpulso in
di questa trasformazione, partendo dalle
precedenti componenti del quadrimpulso in ![]() possiamo trovare quelle in
possiamo trovare quelle in ![]() usando le proprietà generali di trasformazione dei quadrivettori date dalla
(1.23), usando le espressioni di
usando le proprietà generali di trasformazione dei quadrivettori date dalla
(1.23), usando le espressioni di ![]() e
e ![]() in termini di
in termini di ![]() . E' banale verificare che si può scrivere il
quadrimpulso in
. E' banale verificare che si può scrivere il
quadrimpulso in ![]() come:
come:

Il vantaggio di usare
![]() e
e ![]() è che una trasformazione di
Lorentz lungo
è che una trasformazione di
Lorentz lungo ![]() cambia le rapidità di un termine costante da
cambia le rapidità di un termine costante da ![]() a
a
![]() dove
dove ![]() è la rapidità della trasformazione, e così la
configurazione cinematica delle particelle nel sistema del laboratorio
differisce da quella nel centro di massa per un banale spostamento dello zero.
è la rapidità della trasformazione, e così la
configurazione cinematica delle particelle nel sistema del laboratorio
differisce da quella nel centro di massa per un banale spostamento dello zero.