Formulazione lagrangiana del moto di una carica puntiforme

Adesso vogliamo provare ad esprimere in forma analitica le equazioni del moto per una carica puntiforme; dall'espressione (1.83) della forza di Minkowsky dovuta al campo elettromagnetico ottenuta al §1.5.1 si ha che:

$${d{p^i}\over d\tau}={e\over c}F^{i\mu}v_\mu ={e\over c}\left [\pd{\phi^\mu},{x_i}-\pd{\phi^i},{x_\mu}\right]v_\mu$$

adesso però osserviamo che:

$${d{\phi^i}\over d\tau}=\pd{\phi^i},{x_\mu}{d{x_\mu}\over d\tau}=\pd{\phi^i},{x_\mu}v_\mu$$

per cui si ottiene, sostituendo questa nella precedente e portando le derivate rispetto a $\tau$ a primo membro, che:

$${d{}\over d\tau}\left(p^i-{e\over c}\phi^i\right)={e\over c}\pd{\phi^i},{x_\mu}v_\mu$$ (2.102)

Adesso se vogliamo seguire lo schema della meccanica analitica dovremmo riscrivere queste equazioni ricavandole dalla (1.101) allora si verifica subito che se poniamo:

$${\cal L}={1\over 2}m_0 v^\mu v_\mu+{e\over c} \phi^\mu v_\mu$$

la parte spaziale della (1.101) ci da la (1.102).

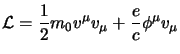
Il secondo membro della (1.101) si calcola immediatamente dato che in $\cal L$ solo $\phi^\mu$ dipende dalle coordinate, per il primo membro dobbiamo sostanzialmente calcolarci la derivata del termine in $v^\mu v_\mu$, dato che l'altro termine è banale; sarà allora:

$$\pd{},{v_\mu}{v^\alpha v_\alpha}=\pd{},{v_\mu}g^{\alpha\beta}v_\a... ...ha g^{\alpha\beta} \delta^\mu_\beta+ v_\beta g^{\alpha\beta} \delta^\mu_\alpha$$

dalla quale si ottiene subito:

$$\pd{},{v_\mu}{v^\alpha v_\alpha} =2 v_\mu$$

dunque l'equazione di Lagrange ci da:

$${d{}\over d\tau}\left( p^\mu+{e\over c} \phi^\mu\right) = {e\over c} \pd{\phi^\nu},{x_\mu} v_\nu$$

la cui parte spaziale ci fornisce subito la (1.102), come volevasi dimostrare.

Si noti che in presenza di un campo elettromagnetico il momento coniugato non è più l'usuale impulso meccanico $p^\mu$ bensì:

$${\mathfrak{p}}^\mu=\pd{\cal L},{v_\mu}=p^\mu+{e\over c} \phi^\mu$$

in cui compare il secondo termine, che esprime l'impulso associato al campo elettromagnetico.