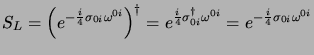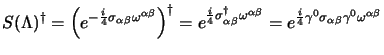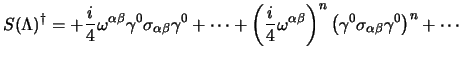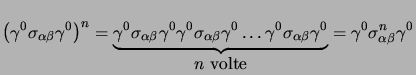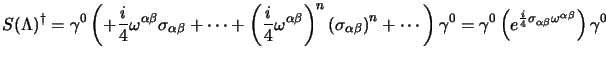Next: La quadricorrente
Up: Covarianza dell'equazione di Dirac
Previous: La prova della covarianza
Contents
Index
Proprietà delle trasformazioni degli spinori
Torneremo sulle trasformazioni improprie più avanti; per ora osserviamo che la
trasformazione (2.34) non è, come nel caso
tridimensionale, unitaria (è una conseguenza della metrica pseudoeuclidea
dello spazio di Minkowsky). Esaminiamo i generatori della trasformazione;
dalla (2.33) si ha che:
e adesso possiamo sfruttare la (2.21) che ci dice che:
da ciò è banale osservare che:
![$\displaystyle (\sigma^{\alpha\beta})^\dagger={i \over 2} \gamma^0[\gamma^\alpha,\gamma^\beta]\gamma^0 = \gamma^0\sigma^{\alpha\beta}\gamma^0$](img697.png) |
(3.35) |
adesso se consideriamo i generatori delle rotazioni tridimensionali questa
diventa:
ma dalle regole di anticommutazione sappiamo che 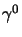 anticommuta con le
anticommuta con le
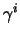 per cui lo si può portare da sinistra a destra anticommutando due
volte (quindi senza cambiare segno) e semplificare, per cui alla fine sia ha:
dunque i generatori delle rotazioni sono hermitiani; se consideriamo invece i
generatori dei boost di Lorentz sarà:
e dunque si vede subito che:
cioè sono antihermitiani.
per cui lo si può portare da sinistra a destra anticommutando due
volte (quindi senza cambiare segno) e semplificare, per cui alla fine sia ha:
dunque i generatori delle rotazioni sono hermitiani; se consideriamo invece i
generatori dei boost di Lorentz sarà:
e dunque si vede subito che:
cioè sono antihermitiani.
Nella rappresentazione di Dirac possiamo calcolare esplicitamente le
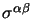 e si ottiene che hanno la forma:
e si ottiene che hanno la forma:
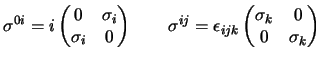 |
(3.36) |
e le proprietà precedenti sono evidenti.
Adesso vediamo cosa succede con le matrici di trasformazione; una prima cosa
che si può vedere è che se consideriamo rotazioni pure  si ha che:
si ha che:
e quindi
 quindi
quindi  è unitaria, mentre se consideriamo
boost di Lorentz puri
è unitaria, mentre se consideriamo
boost di Lorentz puri 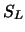 si ha:
dunque
si ha:
dunque
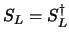 quindi
quindi 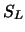 è hermitiana; in generale poi potremo
dare una legge analoga alla (2.35); infatti con essa
possiamo scrivere:
che espansa in serie ci da:
ma evidentemente si ha:
(semplificando i
è hermitiana; in generale poi potremo
dare una legge analoga alla (2.35); infatti con essa
possiamo scrivere:
che espansa in serie ci da:
ma evidentemente si ha:
(semplificando i
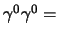 interni) dunque la precedente si può
riscrivere, e raccogliendo tutti i
interni) dunque la precedente si può
riscrivere, e raccogliendo tutti i 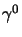 agli estremi, come:
e alla fine si ottiene che:
agli estremi, come:
e alla fine si ottiene che:
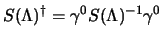 |
(3.37) |
che si può esprimere, in forma equivalente, come:
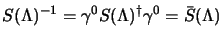 |
(3.38) |
dove
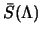 , definita proprio come
, definita proprio come
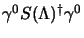 , viene detta aggiunta di
, viene detta aggiunta di
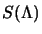 .
.





Next: La quadricorrente
Up: Covarianza dell'equazione di Dirac
Previous: La prova della covarianza
Contents
Index
Simone Piccardi
2003-02-20
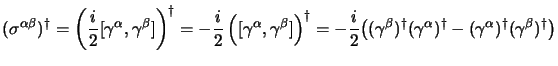
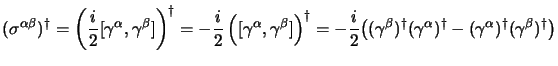
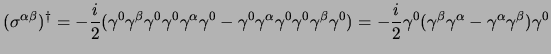
![$\displaystyle (\sigma^{ij})^\dagger={i \over 2}
\gamma^0 [\gamma^i,\gamma^j]\gamma^0
$](img698.png)
![$\displaystyle (\sigma^{0i})^\dagger={i \over 2}
\gamma^0 [\gamma^0,\gamma^i]\ga...
...mma^0\gamma^i\gamma^0\gamma^0)=
{i \over 2}(\gamma^i\gamma^0-\gamma^0\gamma^i)
$](img700.png)
![]() e si ottiene che hanno la forma:
e si ottiene che hanno la forma:
![]() si ha che:
si ha che: