Il campo elettromagnetico.

Abbiamo già visto al §4.3.1 la trattazione lagrangiana covariante delle leggi di Maxwell; la procedura di quantizzazione canonica si applica ai campi $\phi(x)$ standard costruendo i momenti coniugati $\pi(x)$ definiti dalla relazione:

$$\pi(x)=\pd{\cal L},{\dot\phi}$$

analoga a quella per sistemi finiti $p_i=\partial L/\partial \dot q_i$; ovviamente la procedura di quantizzazione si applica quando, come fatto finora, si ha a che fare con campi indipendenti; nel caso del campo elettromagnetico però la trattazione lagrangiana che da le equazioni del moto coinvolge il potenziale $A^\mu$ le cui componenti non sono indipendenti in quanto a causa dell'invarianza di gauge possono essere soggetti a vincoli del tipo delle condizioni di gauge.

Per semplificare le cose tratteremo solo il caso del campo libero; in questo caso la lagrangiana del campo (4.28) si riduce a:

$${\cal L}=-{1\over 4} F^{\mu\nu}F_{\mu\nu}$$

le equazioni del moto, dato che ${\cal L}$ non dipende direttamente dagli $A^\mu$ si riducono a:

$$\partial^\nu \pd{\cal L},{A_{\mu,\nu}}=0$$

dove $A_{\mu,\nu}=\partial_\nu A_\mu$; adesso riscriviamo esplicitamente:

$${\cal L}=-{1\over 4} (A_{\alpha,\beta}-A_{\beta,\alpha}) g^{\alpha\rho} g^{\beta\sigma} (A_{\rho,\sigma}-A_{\sigma,\rho})$$

per cui avremo che:

$$\begin{aligned}\pd{\cal L},{A_{\mu,\nu}} &= - {1\over 4} \big... ...g] \cr &= -F^{\mu\nu}\cr \end{aligned}<tex2html_comment_mark>63$$

dunque le equazioni del moto diventano:

$$\partial^\mu F_{\mu\nu} = 0 = \partial^2 A_\nu-\partial_\nu(\partial^\mu A_\mu) = (g_{\mu\nu}\partial^2-\partial_\mu\partial_\nu) A^\mu$$

se facciamo una trasformazione di gauge $A^\mu\to A^\mu+\partial^\mu \phi$ vediamo subito che queste sono invarianti, infatti:

$$(g_{\mu\nu}\partial^2 - \partial_\mu\partial_\nu) \partial^\mu \phi = \partial_\nu \partial^2 - \partial_\mu\partial_\nu \partial^\mu = 0$$

per la commutabilità delle derivate. Dunque l'operatore d'onda ha un autovettore nullo essendo:

$$(g_{\mu\nu}\partial^2-\partial_\mu\partial_\nu)\partial^\mu =0$$

e questo ci dice che le equazioni del moto non sono indipendenti, infatti essendo $\partial^\mu \partial^\nu$ simmetrico e $F_{\mu\nu}$ antisimmetrico è $\partial^\nu(\partial^\mu F_{\mu\nu})=0$ identicamente.

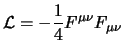
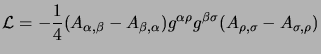
Dalla (5.1) si ottiene subito che l'espressione per gli impulsi canonici è:

$$\Pi^\nu = \pd{\cal L},{\dot A_\nu} = \pd{\cal L},{A_{\nu,0}} = -F^{0\nu} = -\partial^0 A^\nu +\partial^\nu A^0 = -\dot A^\nu +\partial^\nu A^0$$

dunque si ottiene che:

$$\begin{aligned}\Pi^0 &= 0 \cr \Pi^k &= -\dot A^k +\partial^k A^0 = E_k \cr \end{aligned}$$

inoltre si ha che la matrice hessiana del cambiamento di variabile è singolare, infatti dalla (5.1) si ottiene subito che:

$$\begin{aligned} \pd{^2\cal L},{A_{\mu,\nu}\partial A_{\rho,... ...rho\mu} g^{\sigma\nu} + g^{\rho\nu} g^{\sigma\mu} \end{aligned}$$

per cui è banalmente:

$$\pd{^2\cal L},{A_{\mu,0}\partial A_{\nu,0}} = - g^{\nu\mu} g^{00} + g^{\rho 0} g^{0\mu} = - g^{\mu\nu} + g^{0\mu} g^{\nu 0}$$

che è singolare. La prima delle (5.2) da un chiaro vincolo sugli impulsi canonici, inoltre da questa singolarità segue la non invertibilità della relazione fra impulsi e coordinate canoniche; questo dipende dal fatto che essendo componenti di $F^{\mu\nu}$ gli impulsi canonici sono invarianti di gauge, e pertanto non possono dipendere da tutte e quattro le $\dot A^\mu$.

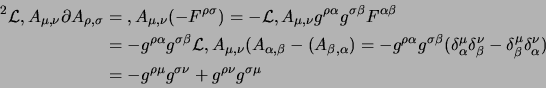
Oltre a questo si ha una ulteriore relazione fra gli impulsi canonici, che è conseguenza delle equazioni del moto, esse infatti si possono scrivere come:

$$\partial^\mu \pd{\cal L},{A_{\nu,\mu}} = \dot \Pi^\nu +\partial_k \pd{\cal L},{A_{\nu,k}} = 0$$

se prendiamo $\nu=0$ da $\Pi^0=0$ segue subito che:

$$\partial_k \pd{\cal L},{A_{0,k}} = -\partial_k F^{k0}=\partial_k F^{0k} = -\pd{\cal L},{A_{k,0}}=-\partial_k \Pi^k=0$$

dunque si ottiene che

$$\partial_k \Pi^k=\nabla\cdot{\bf E}=0$$

questa equazione non coinvolge le derivate temporali e pertanto la si può considerare un ulteriore vincolo che costringe i $\Pi^k$ ad essere a divergenza nulla a qualunque istante.

Il problema che si ha adesso di fronte è quello di come effettuare la quantizzazione di una teoria dove l'invarianza di gauge comporta dei vincoli, usando la procedura standard e mantenendo la covarianza a vista; vedremo che questo è molto complesso e che in realtà si riesce a farlo bene solo con una trattazione diversa da quella seguita finora.

Le strade per effettuare la quantizzazione possono essere diverse, una prima può essere quella di rinunciare alla covarianza a vista per andare a cercare i gradi di libertà effettivi e poi quantizzare quelli con la procedura canonica; si otterranno così una serie di relazioni che non sono né covarianti e né gauge invarianti, e bisognerà poi dimostrare alla fine (cosa tutt'altro che banale) che i risultati ottenuti per le quantità fisiche sono effettivamente covarianti e gauge invarianti.

Un'altra strada è quella di modificare la lagrangiana per avere un momento coniugato non nullo ed usare la quantizzazione ordinaria introducendo dei gradi di libertà fittizi; questo conduce a uno spazio di Hilbert più ampio del voluto (e tra l'altro con metrica indefinita) su cui però si può definire un sottospazio degli stati fisici, conservato nelle interazioni, su cui si va a costruire la teoria, dimostrando che si conserva la covarianza e l'invarianza di gauge.

Una terza strada, che è quella in cui è più facile far emergere la covarianza della teoria, è l'uso del metodo del path integral si ha una formulazione finale estremamente intuitiva, anche se per ottenerla il procedimento è tutt'altro che banale, perché occorre scrivere il path integral prima per una gauge generica in cui ci si sia ridotti ai campi effettivamente indipendenti, e poi tornare indietro agli $A^\mu$ generici con un opportuno procedimento che porti a una covarianza a vista della teoria.

L'espressione generica per il path integral di un campo di lagrangiana ${\cal L}$ è data da:

$$\int {\cal D}(\phi) e^{\displaystyle i\int d^4x {\cal L}(\phi,\partial^\mu \phi)(x)}$$

nel caso del campo elettromagnetico non possiamo scrivere banalmente:

$$\int {\cal D}(A^\mu) e^{\displaystyle i\int d^4x {\cal L}(A^\mu,A^{\mu,\nu})(x)}$$

perché non essendo gli $A^\mu$ indipendenti stiamo sommando anche su gradi di libertà fittizi e questa espressione non ha più significato. Dovremmo allora ridurci ai soli gradi di libertà indipendenti fissando una condizione di gauge $g(A^\mu)=0$.

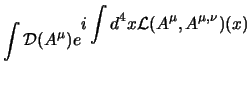
L'idea è che se introduciamo la delta di Dirac funzionale, cioè il funzionale $\delta[\phi]$ tale che:

$$\int {\cal D}(\phi) \delta[\phi] F[\phi] = F[0]$$

in maniera molto ingenua possiamo cancellare i gradi di libertà fittizi nel path integral scrivendolo semplicemente come:

$$\int {\cal D}(A^\mu) \delta[g] e^{\displaystyle i\int d^4x {\cal L}(A^\mu,A^{\mu,\nu})(x)}$$

e basta prendere una condizione di gauge covariante (come la gauge di Lorentz) per avere la covarianza a vista della teoria.

Questa è effettivamente la formula che si ottiene, ma bisogna mostrare che la procedura è corretta partendo da ciò che si sa essere corretto, cioè il path integral applicato a campi indipendenti.