




Next: Il teorema della Noeter.
Up: La meccanica analitica dei
Previous: La meccanica analitica dei
Contents
Index
Il formalismo lagrangiano della teoria dei campi.
Vediamo allora come si può formulare una trattazione generale della dinamica
dei campi. Il punto di partenza resta il principio di minima azione, si dovrà
però vedere come riesprimere l'azione avendo a che fare con campi; comunque se
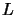 è la lagrangiana del sistema sarà ancora:
è la lagrangiana del sistema sarà ancora:
soltanto che adesso l'espressione di 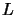 si otterrà (essendo il
limite continuo delle somme delle lagrangiane di ogni grado di libertà) come
integrale di una densità di lagrangiana
si otterrà (essendo il
limite continuo delle somme delle lagrangiane di ogni grado di libertà) come
integrale di una densità di lagrangiana 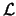 ; e nel caso generale,
essendo in tre dimensioni, sarà:
ed
; e nel caso generale,
essendo in tre dimensioni, sarà:
ed 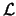 in generale sarà, per quanto visto prima e per analogia con la
meccanica analitica classica, funzione dei campi, delle loro derivate spaziali
e temporali, ed eventualmente anche delle coordinate (spaziali e temporali),
ma quest'ultimo caso sarà solo quello in cui agiscono forze esterne; in
generale se considereremo solo campi liberi o al più interagenti fra di loro,
l'omogeneità ed isotropia dello spazio e del tempo ci permette di escludere
questa dipendenza che automaticamente privilegerebbe istanti e coordinate
particolari.
in generale sarà, per quanto visto prima e per analogia con la
meccanica analitica classica, funzione dei campi, delle loro derivate spaziali
e temporali, ed eventualmente anche delle coordinate (spaziali e temporali),
ma quest'ultimo caso sarà solo quello in cui agiscono forze esterne; in
generale se considereremo solo campi liberi o al più interagenti fra di loro,
l'omogeneità ed isotropia dello spazio e del tempo ci permette di escludere
questa dipendenza che automaticamente privilegerebbe istanti e coordinate
particolari.
Utilizzando tutto ciò potremo allora riscriverci l'azione nella forma più
generale (considerando anche più campi
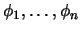 ) come:
) come:
è immediato notare che questo è un integrale quadridimensionale, per cui è
immediato impostare tutto col formalismo relativistico, facendo direttamente
una teoria covariante.
Il punto fondamentale è allora che si postula che anche in relatività resti
valido il principio di minima azione, per cui esiste una quantità 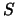 (che
deve essere un invariante) la cui variazione, nel senso che preciseremo
subito, deve essere nulla sul moto effettivo; l'analogia col caso classico ci
permette di usare la formulazione appena data, che riscriveremo in forma
relativistica come:
(che
deve essere un invariante) la cui variazione, nel senso che preciseremo
subito, deve essere nulla sul moto effettivo; l'analogia col caso classico ci
permette di usare la formulazione appena data, che riscriveremo in forma
relativistica come:
 |
(5.4) |
dove l'integrale si prende sul volume compreso fra due superfici space-like
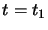 e
e  , ma può essere comunque essere definito anche più in
generale. Questa definizione ci mostra anche che la densità di lagrangiana
deve essere uno scalare invariante.
, ma può essere comunque essere definito anche più in
generale. Questa definizione ci mostra anche che la densità di lagrangiana
deve essere uno scalare invariante.
Adesso per trovare le equazioni del moto dovremo applicare il principio di
Hamilton che dice che  è nullo per tutti gli spostamenti virtuali
che lasciano invariati gli estremi; tali spostamenti però riguardano solo i
campi
è nullo per tutti gli spostamenti virtuali
che lasciano invariati gli estremi; tali spostamenti però riguardano solo i
campi  (che sono gli equivalenti delle
(che sono gli equivalenti delle  dei sistemi finiti) e non
le coordinate spaziali che qui fungono da indici e che quindi, come il tempo
nella meccanica analitica classica, resteranno costanti, per cui la variazione
non può influire né sui limiti di integrazione rispetto al tempo, né sulla
regione di integrazione spaziale, ma sarà data solo dalla variazione della
densità di lagrangiana dovuta al variare dei campi.
dei sistemi finiti) e non
le coordinate spaziali che qui fungono da indici e che quindi, come il tempo
nella meccanica analitica classica, resteranno costanti, per cui la variazione
non può influire né sui limiti di integrazione rispetto al tempo, né sulla
regione di integrazione spaziale, ma sarà data solo dalla variazione della
densità di lagrangiana dovuta al variare dei campi.
Oltre a questo la condizione di variazione nulla sugli estremi significherà in
questo caso le variazioni dei campi dovranno essere nulle sulla ipersuperficie
(tridimensionale) che contorna l'ipervolume su cui si integra, cioè sia per
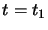 e
e  che all'infinito; sarà cioè:
che all'infinito; sarà cioè:
 |
(5.5) |
fatte queste considerazioni possiamo passare a calcolarci la variazione
dell'azione che sarà:
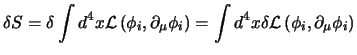 |
(5.6) |
per cui basta calcolarsi la variazione di 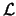 ; per snellire le formule
introduciamo la notazione
; per snellire le formule
introduciamo la notazione
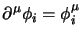 , sarà allora:
dove per definizione:
e si è sottintesa la somma sugli indici ripetuti. Adesso con queste
relazioni la (4.6) diventa:
adesso possiamo integrare per parti il secondo addendo, otterremo:
ma le condizioni (4.5) di
variazioni nulle agli estremi ci dicono che
, sarà allora:
dove per definizione:
e si è sottintesa la somma sugli indici ripetuti. Adesso con queste
relazioni la (4.6) diventa:
adesso possiamo integrare per parti il secondo addendo, otterremo:
ma le condizioni (4.5) di
variazioni nulle agli estremi ci dicono che
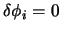 su
su 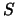 dunque
di questa resta solo il secondo termine che sostituito nella precedente ci da:
(si è raccolto
dunque
di questa resta solo il secondo termine che sostituito nella precedente ci da:
(si è raccolto
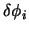 ) adesso
) adesso  e tutti i
e tutti i
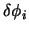 sono
indipendenti ed arbitrari per cui per far si che sia nullo l'integrale deve
essere nullo l'integrando e dunque si ottengono le equazioni:
sono
indipendenti ed arbitrari per cui per far si che sia nullo l'integrale deve
essere nullo l'integrando e dunque si ottengono le equazioni:
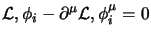 |
(5.7) |
che sono tante quanti sono i campi e ci danno la dinamica dei medesimi;
anch'esse, come generalizzazione al caso con infiniti gradi di libertà, sono
dette equazioni di Eulero-Lagrange, per i campi.
Si noti che se si aggiunge alla densità di lagrangiana (da qui in avanti per
semplicità la chiameremo direttamente lagrangiana) la divergenza di una
funzione qualsiasi dei campi:
l'azione, per il teorema di Gauss, non varia, dunque anche le
(4.7) sono invarianti, questo si può vedere direttamente
se sostituiamo questa espressione a 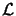 nella
(4.7) verificando che il risultato è identicamente nullo;
infatti:
nella
(4.7) verificando che il risultato è identicamente nullo;
infatti:





Next: Il teorema della Noeter.
Up: La meccanica analitica dei
Previous: La meccanica analitica dei
Contents
Index
Simone Piccardi
2003-02-20
![]() è la lagrangiana del sistema sarà ancora:
è la lagrangiana del sistema sarà ancora:


![]() ) come:
) come:
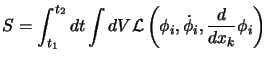
![]() (che
deve essere un invariante) la cui variazione, nel senso che preciseremo
subito, deve essere nulla sul moto effettivo; l'analogia col caso classico ci
permette di usare la formulazione appena data, che riscriveremo in forma
relativistica come:
(che
deve essere un invariante) la cui variazione, nel senso che preciseremo
subito, deve essere nulla sul moto effettivo; l'analogia col caso classico ci
permette di usare la formulazione appena data, che riscriveremo in forma
relativistica come:
![]() è nullo per tutti gli spostamenti virtuali
che lasciano invariati gli estremi; tali spostamenti però riguardano solo i
campi
è nullo per tutti gli spostamenti virtuali
che lasciano invariati gli estremi; tali spostamenti però riguardano solo i
campi ![]() (che sono gli equivalenti delle
(che sono gli equivalenti delle ![]() dei sistemi finiti) e non
le coordinate spaziali che qui fungono da indici e che quindi, come il tempo
nella meccanica analitica classica, resteranno costanti, per cui la variazione
non può influire né sui limiti di integrazione rispetto al tempo, né sulla
regione di integrazione spaziale, ma sarà data solo dalla variazione della
densità di lagrangiana dovuta al variare dei campi.
dei sistemi finiti) e non
le coordinate spaziali che qui fungono da indici e che quindi, come il tempo
nella meccanica analitica classica, resteranno costanti, per cui la variazione
non può influire né sui limiti di integrazione rispetto al tempo, né sulla
regione di integrazione spaziale, ma sarà data solo dalla variazione della
densità di lagrangiana dovuta al variare dei campi.
![]() e
e ![]() che all'infinito; sarà cioè:
che all'infinito; sarà cioè:
![$\displaystyle \delta S
= \int d^4x
\left[
\pd{\cal L},{\phi_i} \delta \phi_i
+ \pd{\cal L},{\phi_i^\mu} \partial^\mu \delta \phi_i
\right]
$](img1682.png)
![$\displaystyle \int d^4x
\pd{\cal L},{\phi_i^\mu} \partial^\mu \delta \phi_i
=...
...int d^4x
\left[
\partial^\mu \pd{\cal L},{\phi_i^\mu}
\right] \delta \phi_i
$](img1683.png)
![$\displaystyle \delta S
= \int d^4x
\left[
\pd{\cal L},{\phi_i}
- \left(
\partial^\mu \pd{\cal L},{\phi_i^\mu}
\right)
\right]
\delta\phi_i
$](img1685.png)