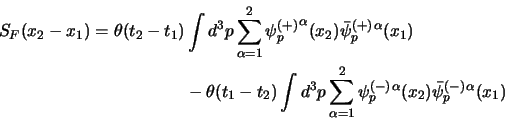Next: Le equazioni di propagazione
Up: Il propagatore in meccanica
Previous: Il propagatore libero per
Contents
Index
La prescrizione di Feynmann
Quanto abbiamo appena visto ci dice che per come è messa la struttura
dell'equazione di Dirac, la presenza delle soluzioni ad energia negativa unita
all'ipotesi del mare di Dirac ci costringe a cambiare le condizioni al
contorno che adesso non sono più, come nel caso classico, che esso sia nullo
per tempi antecedenti per evitare problemi di causalità, ma che esso propaghi
in avanti nel tempo solo soluzioni ad energia positiva, ed indietro nel tempo
solo soluzioni ad energia negativa.
Adesso possiamo vedere come questa condizione (detta anche
prescrizione di Feynmann) si esprime nel calcolo dell'espressione del
propagatore libero che si effettua usando le trasformate di Fourier. Il punto
di partenza è la (3.18), che essendo invariante per
traslazione ci permette di considerare che
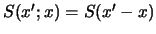 per cui potremo
espanderlo con le trasformate di Fourier come funzione di
per cui potremo
espanderlo con le trasformate di Fourier come funzione di 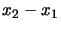 . Adesso
per semplificare le equazioni introdurremo da qui in avanti le unità di misura
naturali, le unità cioè per le quali vale
. Adesso
per semplificare le equazioni introdurremo da qui in avanti le unità di misura
naturali, le unità cioè per le quali vale  ; scriveremo
così:
; scriveremo
così:
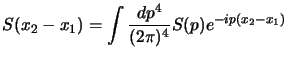 |
(4.20) |
e dovremo ricordarci alla fine di rimettere tutti gli 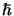 ed i
ed i 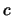 necessari per far tornare le dimensioni.
necessari per far tornare le dimensioni.
Adesso possiamo procedere come al paragrafo precedente usando la
(3.18); otterremo l'equazione per il propagatore:
che portando le derivate sotto l'integrale ci da:
da cui si ottiene l'equazione algebrica:
(si ricordi che ovviamente in questo caso
 è una matrice
è una matrice
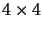 ) adesso qui si può fare una divisione formale per
) adesso qui si può fare una divisione formale per 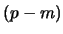 ,
intesa nel senso di moltiplicare per la matrice inversa, questa però è una
matrice singolare, per vedere allora cosa viene fuori, senza stare a
complicarsi la vita con l'inversione delle matrici, notiamo che se
moltiplichiamo questa per
,
intesa nel senso di moltiplicare per la matrice inversa, questa però è una
matrice singolare, per vedere allora cosa viene fuori, senza stare a
complicarsi la vita con l'inversione delle matrici, notiamo che se
moltiplichiamo questa per 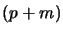 si ha:
e adesso si può fare una semplice divisione numerica, ottenendo che, per
si ha:
e adesso si può fare una semplice divisione numerica, ottenendo che, per
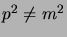 , si ha:
, si ha:
Adesso come prima occorre stabilire cosa succede per
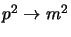 assegnando le
condizioni al contorno, solo che adesso i poli sono due e corrispondono ai due
possibili valori dell'energia:
assegnando le
condizioni al contorno, solo che adesso i poli sono due e corrispondono ai due
possibili valori dell'energia:
e se utilizziamo questa possiamo scrivere l'espressione della trasformata
di Fourier in (3.20), spezzando ancora
l'integrale, come:
anche qui è possibile imporre che il propagatore propaghi solo in avanti
nel tempo sostituendo a  la quantità
la quantità
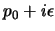 in modo che entrambi
i poli si spostino appena sotto l'asse reale e sopravviva solo la parte con
in modo che entrambi
i poli si spostino appena sotto l'asse reale e sopravviva solo la parte con
 ; avremo così la funzione di Green ritardata per l'equazione di
Dirac data da:
solo che stavolta per la fisica non ci interessa questa, quanto il propagatore
di Feynmann
; avremo così la funzione di Green ritardata per l'equazione di
Dirac data da:
solo che stavolta per la fisica non ci interessa questa, quanto il propagatore
di Feynmann
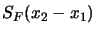 che propaga in avanti nel tempo le soluzioni ad
energia positiva ed indietro quelle ad energia negativa; questo si può
ottenere se aggiungiamo
che propaga in avanti nel tempo le soluzioni ad
energia positiva ed indietro quelle ad energia negativa; questo si può
ottenere se aggiungiamo 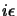 al polo ad energia positiva e
al polo ad energia positiva e
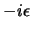 a quello ad energia negativa; prenderemo cioè:
in questo caso si può verificare banalmente che il lemma di Jordan farà
sopravvivere solo la parte ad energia positiva per
a quello ad energia negativa; prenderemo cioè:
in questo caso si può verificare banalmente che il lemma di Jordan farà
sopravvivere solo la parte ad energia positiva per
 e quella ad
energia negativa per
e quella ad
energia negativa per 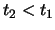 .
.
Per eseguire il calcolo conviene usare al posto di
 , che è una
matrice, la funzione di Green
, che è una
matrice, la funzione di Green
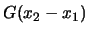 dell'equazione di Klein-Gordon
definita da:
dell'equazione di Klein-Gordon
definita da:
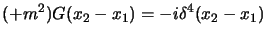 |
(4.21) |
con questa è banale verificare che se prendiamo:
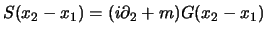 |
(4.22) |
otteniamo una soluzione della (3.18); d'altra parte
risolvendo la (3.21) con le trasformate di
Fourier si ottiene l'equazione algebrica (basta eseguire i conti e
semplificare un segno meno):
per cui poi ci si ritrova con una funzione con le stesse singolarità di
 , e che quindi possiamo trattare allo stesso modo, per cui potremo
ottenere la soluzione con le corrette condizioni al contorno come:
, e che quindi possiamo trattare allo stesso modo, per cui potremo
ottenere la soluzione con le corrette condizioni al contorno come:
Figure 3.4:
I due cammini su cui si applica il Lemma di Jordan per il calcolo
dell'integrale del propagatore con la prescrizione di Feynmann.
|
|
Adesso cominciamo col caso
 ; in tal caso per usare il lemma di
Jordan dovremo chiudere l'integrale con un semicerchio all'infinito per
; in tal caso per usare il lemma di
Jordan dovremo chiudere l'integrale con un semicerchio all'infinito per 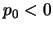 ed essendo in tal caso l'integrale sulla retta reale all'inverso
rispetto al senso antiorario otterremo:
ed essendo in tal caso l'integrale sulla retta reale all'inverso
rispetto al senso antiorario otterremo:
(si è semplificato un 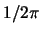 nell'integrale col
nell'integrale col  che viene dal
lemma di Jordan) adesso il calcolo del residuo è immediato:
per cui alla fine si ottiene che:
se poi consideriamo il caso
che viene dal
lemma di Jordan) adesso il calcolo del residuo è immediato:
per cui alla fine si ottiene che:
se poi consideriamo il caso 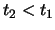 dobbiamo chiudere l'integrale nel
semipiano
dobbiamo chiudere l'integrale nel
semipiano 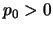 , ed otterremo:
(il segno è opposto perché l'integrale sulla retta reale è nel senso giusto) ed
il residuo stavolta è:
per cui si ottiene che:
per cui alla fine, unendo i due termini, si ha la definitiva:
che vale per tempi qualsiasi.
, ed otterremo:
(il segno è opposto perché l'integrale sulla retta reale è nel senso giusto) ed
il residuo stavolta è:
per cui si ottiene che:
per cui alla fine, unendo i due termini, si ha la definitiva:
che vale per tempi qualsiasi.
Si noti che questa espressione soddisfa le condizioni al contorno richieste,
dato che per
 si propagano solo energia positive, mentre per
si propagano solo energia positive, mentre per
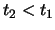 si propagano solo energia negative; si noti anche come
nell'integrale compaia una misura invariante proporzionale (manca
si propagano solo energia negative; si noti anche come
nell'integrale compaia una misura invariante proporzionale (manca 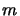 ) alla
) alla
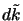 già menzionata nel §2.4.4 in
(2.112). Considerato questo l'espressione
precedente può essere espressa in forma covariante a vista; infatti
l'integrazione su
già menzionata nel §2.4.4 in
(2.112). Considerato questo l'espressione
precedente può essere espressa in forma covariante a vista; infatti
l'integrazione su  non cambia se mandiamo p in
non cambia se mandiamo p in 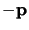 , per cui
se lo facciamo per il secondo addendo in parentesi quadra si ottiene:
, per cui
se lo facciamo per il secondo addendo in parentesi quadra si ottiene:
che è covariante a vista.
Adesso possiamo passare a
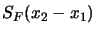 usando l'espressione
(3.23) di
usando l'espressione
(3.23) di
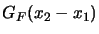 appena trovata, e la
relazione (3.22); si ottiene subito
che:
appena trovata, e la
relazione (3.22); si ottiene subito
che:
che banalmente si può riscrivere come:
dove
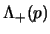 e
e
 sono i proiettori sugli stati ad
energia positiva e negativa visti in (2.89) al
§2.4.3; da questa, usando le espressioni alternative dei
proiettori in termini degli spinori di (2.88), si ha:
che, usando le espressioni
(2.110) per le autofunzioni
normalizzate dell'equazione di Dirac libera, diventa subito:
che è esattamente la forma della (3.19).
sono i proiettori sugli stati ad
energia positiva e negativa visti in (2.89) al
§2.4.3; da questa, usando le espressioni alternative dei
proiettori in termini degli spinori di (2.88), si ha:
che, usando le espressioni
(2.110) per le autofunzioni
normalizzate dell'equazione di Dirac libera, diventa subito:
che è esattamente la forma della (3.19).





Next: Le equazioni di propagazione
Up: Il propagatore in meccanica
Previous: Il propagatore libero per
Contents
Index
Simone Piccardi
2003-02-20
![]() per cui potremo
espanderlo con le trasformate di Fourier come funzione di
per cui potremo
espanderlo con le trasformate di Fourier come funzione di ![]() . Adesso
per semplificare le equazioni introdurremo da qui in avanti le unità di misura
naturali, le unità cioè per le quali vale
. Adesso
per semplificare le equazioni introdurremo da qui in avanti le unità di misura
naturali, le unità cioè per le quali vale ![]() ; scriveremo
così:
; scriveremo
così:
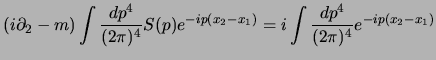


![]() assegnando le
condizioni al contorno, solo che adesso i poli sono due e corrispondono ai due
possibili valori dell'energia:
assegnando le
condizioni al contorno, solo che adesso i poli sono due e corrispondono ai due
possibili valori dell'energia:
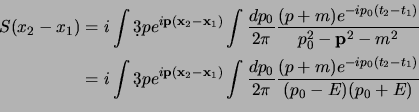
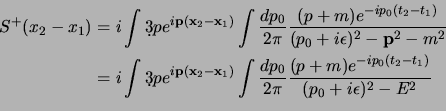

![]() , che è una
matrice, la funzione di Green
, che è una
matrice, la funzione di Green
![]() dell'equazione di Klein-Gordon
definita da:
dell'equazione di Klein-Gordon
definita da:
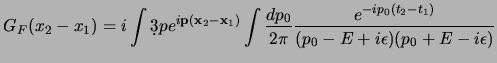
![\includegraphics[width=14cm]{fig_4_4}](img1493.png)
![]() ; in tal caso per usare il lemma di
Jordan dovremo chiudere l'integrale con un semicerchio all'infinito per
; in tal caso per usare il lemma di
Jordan dovremo chiudere l'integrale con un semicerchio all'infinito per ![]() ed essendo in tal caso l'integrale sulla retta reale all'inverso
rispetto al senso antiorario otterremo:
ed essendo in tal caso l'integrale sulla retta reale all'inverso
rispetto al senso antiorario otterremo:
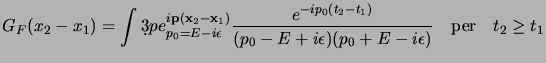
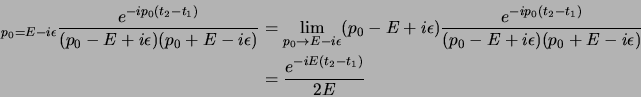
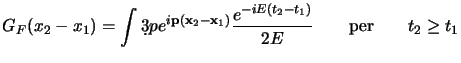
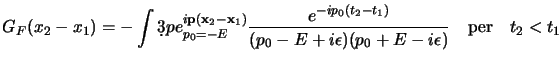
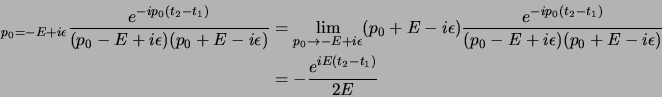

![$\displaystyle G_F(x_2-x_1)
= \int {d^3p\over 2E(2\pi)^3}
e^{i{\bf p}({\bf x}_2...
...\left[
\theta(t_2-t_1)e^{-iE(t_2-t_1)}+
\theta(t_1-t_2)e^{iE(t_2-t_1)}
\right]
$](img1504.png)
![]() si propagano solo energia positive, mentre per
si propagano solo energia positive, mentre per
![]() si propagano solo energia negative; si noti anche come
nell'integrale compaia una misura invariante proporzionale (manca
si propagano solo energia negative; si noti anche come
nell'integrale compaia una misura invariante proporzionale (manca ![]() ) alla
) alla
![]() già menzionata nel §2.4.4 in
(2.112). Considerato questo l'espressione
precedente può essere espressa in forma covariante a vista; infatti
l'integrazione su
già menzionata nel §2.4.4 in
(2.112). Considerato questo l'espressione
precedente può essere espressa in forma covariante a vista; infatti
l'integrazione su ![]() non cambia se mandiamo p in
non cambia se mandiamo p in ![]() , per cui
se lo facciamo per il secondo addendo in parentesi quadra si ottiene:
, per cui
se lo facciamo per il secondo addendo in parentesi quadra si ottiene:
![]() usando l'espressione
(3.23) di
usando l'espressione
(3.23) di
![]() appena trovata, e la
relazione (3.22); si ottiene subito
che:
appena trovata, e la
relazione (3.22); si ottiene subito
che:
![\begin{displaymath}
\begin{aligned}
S_F(x_2-x_1)
&= (i\s{\partial}_2+m) G_F(x_...
...ta(t_1-t_2)(m-\s{p}) e^{ip(x_2-x_1)}
\right]\cr
\end{aligned}\end{displaymath}](img1508.png)
![\begin{displaymath}
\begin{aligned}
S_F(x_2-x_1)
&= \int {d^3p\over(2\pi)^3}{2...
...t_1-t_2)\Lambda_-(p) e^{ip(x_2-x_1)}
\right]\cr
\end{aligned}\end{displaymath}](img1509.png)
![\begin{displaymath}
\begin{aligned}
S_F(x_2-x_1)
= \int {d^3p\over(2\pi)^3} {m...
...bar v^{(\alpha)}(p) e^{ip(x_2-x_1)}
\right] \cr
\end{aligned}\end{displaymath}](img1512.png)