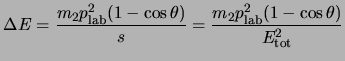Dalle precedenti relazioni cinematiche e dal principio di conservazione
dell'energia-impulso (cioè di ![]() ) si possono ricavare delle
caratteristiche generali della dinamica delle particelle (in particolare nei
casi di urto e decadimento) anche se non è noto il tipo di interazione.
) si possono ricavare delle
caratteristiche generali della dinamica delle particelle (in particolare nei
casi di urto e decadimento) anche se non è noto il tipo di interazione.
Per snellire la scrittura delle equazioni per il seguito di questo paragrafo
useremo le cosiddette unità naturali, cioè misureremo tutto in
termini di velocità della luce per cui nelle formule sarà ![]() ; il
quadrimpulso diventerà
; il
quadrimpulso diventerà
![]() e la relazione di Einstein
(1.50) si potrà semplificare in
e la relazione di Einstein
(1.50) si potrà semplificare in
![]() .
.
Cominciamo con il caso generale di urto di due particelle: non ci interessa la
dinamica dell'urto, consideriamo solo due particelle incidenti di quadrimpulso
![]() e
e
![]() e masse
e masse ![]() e
e ![]() e due
particelle diffuse di impulso
e due
particelle diffuse di impulso
![]() e
e
![]() e
masse
e
masse ![]() e
e ![]() e in generale sarà
e in generale sarà
![]() .
.
La conservazione del quadrimpulso, che è una legge assolutamente generale, ci dice che in ogni caso dovrà essere:
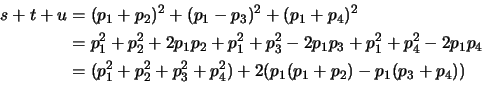
![\includegraphics[width=13cm]{fig_1_1}](img259.png)
|
Sono di particolare importanza nei calcoli relativistici due sistemi di
riferimento particolari: quello del laboratorio (in cui si suppone il
bersaglio fermo), nel quale vale
![]() ,
,
![]() e quello del centro di massa, in cui vale
e quello del centro di massa, in cui vale
![]() e
e
![]() ed anche, per la conservazione del
quadrimpulso,
ed anche, per la conservazione del
quadrimpulso,
![]() e
e
![]() (vedi
fig. 1.2).
(vedi
fig. 1.2).
La definizione precedente ci mostra subito che ![]() è l'energia totale
nel sistema del baricentro, dato che in esso è banalmente
è l'energia totale
nel sistema del baricentro, dato che in esso è banalmente
![]() ; questa è molto importante, perché è l'energia
disponibile per le reazioni; nel caso che si abbia a che fare con urti di un
fascio su un bersaglio questa si può esprimere in termini dell'energia della
particella incidente (cioè nel sistema di laboratorio); si ha infatti che:
; questa è molto importante, perché è l'energia
disponibile per le reazioni; nel caso che si abbia a che fare con urti di un
fascio su un bersaglio questa si può esprimere in termini dell'energia della
particella incidente (cioè nel sistema di laboratorio); si ha infatti che:
Un'altra relazione importante è quella che lega
![]() a
a
![]() ; per ottenerla consideriamo che siccome il prodotto scalare è
invariante si ha:
; per ottenerla consideriamo che siccome il prodotto scalare è
invariante si ha:
Un caso particolare di grande interesse è poi quello dell'urto elastico, in cui
cioè le particelle restano le stesse prima e dopo l'urto; si ha cioè che
![]() e
e ![]() e dunque
e dunque
![]() e
e
![]() .
.
La prima relazione interessante si ha quando si va a calcolare l'energia
cinetica trasferita (cioè l'energia cinetica trasferita a ![]() nell'urto) che nel sistema del laboratorio è data banalmente da
nell'urto) che nel sistema del laboratorio è data banalmente da
![]() ; per farlo basta calcolare il valore della variabile di Mandelstam
; per farlo basta calcolare il valore della variabile di Mandelstam
![]() nel sistema del laboratorio, che con le notazioni adottate è:
nel sistema del laboratorio, che con le notazioni adottate è:
Una relazione fondamentale valida per gli urti elastici è che deve essere
![]() ; in un urto elastico cioè l'impulso nel sistema di laboratorio può solo
cambiare direzione; questa si dimostra partendo dal fatto che, per come lo
abbiamo definito, in un urto elastico si ha:
; in un urto elastico cioè l'impulso nel sistema di laboratorio può solo
cambiare direzione; questa si dimostra partendo dal fatto che, per come lo
abbiamo definito, in un urto elastico si ha:
| (2.58a) |
A questo punto se usiamo la (1.57) possiamo trovare un'altra
espressione più utile per ![]() ; infatti se ci calcoliamo
; infatti se ci calcoliamo ![]() nel sistema
del centro di massa otteniamo che:
nel sistema
del centro di massa otteniamo che:
![$\displaystyle \Delta E=-{1\over 2m_2}[m_1^2 +m_1^2-2(E_1E_3-pq\cos{\theta})]
$](img307.png)
![$\displaystyle \Delta E=-{1\over 2m_2}[2m_1^2 -2(E_1^2-p^2\cos{\theta})]=
-{1\over 2m_2}[2m_1^2 - 2(m_1^2+p^2-p^2\cos{\theta})]
$](img309.png)