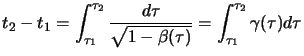



Next: La quadriaccelerazione
Up: Cinematica relativistica
Previous: Cinematica relativistica
Contents
Index
La quadrivelocità
Non si può definire la velocità come 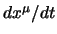 perché
perché 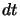 non è invariante,
e questo non sarebbe un quadrivettore; dobbiamo seguire allora un'altra
strada. Conosciamo però un invariante fondamentale che è l'elemento di linea:
non è invariante,
e questo non sarebbe un quadrivettore; dobbiamo seguire allora un'altra
strada. Conosciamo però un invariante fondamentale che è l'elemento di linea:
per cui è possibile definire un quadrivettore:
ma questa non ha le dimensioni giuste; notiamo allora che:
da cui segue immediatamente che:
e da questa si vede subito, dato che 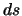 e
e 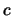 sono invarianti, che se
definiamo:
sono invarianti, che se
definiamo:
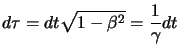 |
(2.34) |
si ottiene un invariante con le dimensioni di un tempo. Più precisamente si
può notare che questo è il tempo che segna l'orologio solidale con una
particella in moto (nel sistema solidale 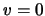 e quindi
e quindi
 ) ed è
per questo chiamato tempo proprio.
) ed è
per questo chiamato tempo proprio.
Si noti che in un qualsiasi sistema di riferimento 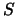 un certo intervallo di
tempo proprio
un certo intervallo di
tempo proprio 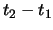 verrà misurato integrando l'inversa della
(1.34), cioè sarà:
verrà misurato integrando l'inversa della
(1.34), cioè sarà:
e questa ci mostra l'effetto noto come dilatazione del tempo, infatti
per una particella in moto a velocità costante si ha la relazione
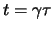 .
.
Con il tempo proprio possiamo definire un quadrivettore con le dimensioni
corrispondenti a quelle di una velocità, che chiameremo appunto
quadrivelocità:
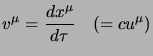 |
(2.35) |
e se usiamo la (1.34) otteniamo subito che:
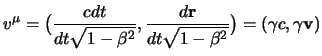 |
(2.36) |
e si vede subito che, contrariamente a
 ,
,
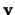 non è la
parte spaziale di un quadrivettore, mentre lo è
non è la
parte spaziale di un quadrivettore, mentre lo è
 , per cui
non è affatto immediata l'identificazione di
, per cui
non è affatto immediata l'identificazione di 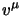 come una velocità
ordinaria.
come una velocità
ordinaria.




Next: La quadriaccelerazione
Up: Cinematica relativistica
Previous: Cinematica relativistica
Contents
Index
Simone Piccardi
2003-02-20
![]() perché
perché ![]() non è invariante,
e questo non sarebbe un quadrivettore; dobbiamo seguire allora un'altra
strada. Conosciamo però un invariante fondamentale che è l'elemento di linea:
non è invariante,
e questo non sarebbe un quadrivettore; dobbiamo seguire allora un'altra
strada. Conosciamo però un invariante fondamentale che è l'elemento di linea:


![]() un certo intervallo di
tempo proprio
un certo intervallo di
tempo proprio ![]() verrà misurato integrando l'inversa della
(1.34), cioè sarà:
verrà misurato integrando l'inversa della
(1.34), cioè sarà: