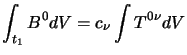Next: Cinematica relativistica
Up: Nozioni base di relatività
Previous: Cenni di analisi tensoriale
Contents
Index
Teorema della divergenza e correnti conservate
Vogliamo infine dimostrare un utile teorema, conseguenza diretta del teorema
della divergenza; sia 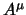 un vettore a divergenza nulla; cioè:
un vettore a divergenza nulla; cioè:
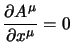 |
(2.31) |
e tale che
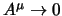 per
per
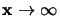 ; il teorema afferma che in tal
caso la quantità:
è uno scalare costante nel tempo.
; il teorema afferma che in tal
caso la quantità:
è uno scalare costante nel tempo.
La dimostrazione si fa col teorema di Gauss, che in uno spazio di Minkowsky,
può essere espresso come:
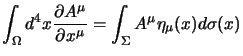 |
(2.32) |
dove 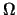 è un volume quadridimensionale qualsiasi e
è un volume quadridimensionale qualsiasi e  è la
superficie che lo racchiude (che è uno spazio a tre dimensioni).
è la
superficie che lo racchiude (che è uno spazio a tre dimensioni).
Adesso prendiamo come ipervolume 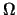 quello compreso fra due
ipersuperfici a
quello compreso fra due
ipersuperfici a  costante e pari a
costante e pari a  e
e 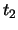 (vedi 1.1), per tali superfici, con la convenzione di normale
esterna si ha:
(vedi 1.1), per tali superfici, con la convenzione di normale
esterna si ha:
(e si noti che i corrispondenti versori covarianti sono uguali a questi
perché la parte spaziale è nulla), mentre
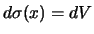 e l'integrale su
e l'integrale su
 si estende a tutto lo spazio ordinario; così la
(1.32) ci da:
dato che l'integrale sulla parte all'infinito che chiude le due
ipersuperfici a
si estende a tutto lo spazio ordinario; così la
(1.32) ci da:
dato che l'integrale sulla parte all'infinito che chiude le due
ipersuperfici a  e
e 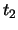 si annulla poiché
si annulla poiché
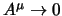 per
per
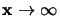 . Adesso il primo termine di questa è a sua volta è nullo per la
(1.31), e quindi alla fine si ottiene che:
e fata l'arbitrarietà di
. Adesso il primo termine di questa è a sua volta è nullo per la
(1.31), e quindi alla fine si ottiene che:
e fata l'arbitrarietà di  e
e 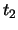 questo integrale è lo stesso a
qualunque tempo lo si calcoli.
questo integrale è lo stesso a
qualunque tempo lo si calcoli.
Ma se consideriamo una qualunque trasformazione di Lorentz applicata a questo
integrale, tutto quello che essa potrà variare, dato che la dipendenza dalle
coordinate spaziali sparisce integrando su tutto lo spazio, è il valore del
tempo, ma abbiamo appena visto che il valore dell'integrale è sempre lo stesso
quindi, come volevasi dimostrare, abbiamo un invariante.
Figure 1.1:
Proiezione sugli assi 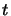 e
e 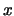 delle
due quadrisuperfici a
delle
due quadrisuperfici a 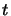 costante e pari a
costante e pari a  e
e 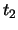 .
.
|
|
Il risultato dimostrato per un quadrivettore si può generalizzare in maniera
semplice nel caso di divergenze nulle di tensori di qualunque ordine;
consideriamo ad esempio che sia:
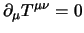 |
(2.33) |
in tal caso otterremo che la quantità conservata è il quadrivettore:
Questo lo possiamo dimostrare sfruttando il risultato precedente; prendiamo un
qualunque quadrivettore costante 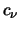 e definiamo
e definiamo
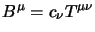 ,
dalla (1.33) si ottiene subito che:
,
dalla (1.33) si ottiene subito che:
per cui per quanto visto prima:
è un invariante, quindi per le proprietà di trasformazione di 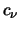 si
ottiene quanto volevamo. Si noti anche che, dato che
si
ottiene quanto volevamo. Si noti anche che, dato che 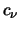 è un
quadrivettore costante, deve esserlo pure
è un
quadrivettore costante, deve esserlo pure 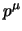 . L'estensione ad ordini
superiori è identica.
. L'estensione ad ordini
superiori è identica.





Next: Cinematica relativistica
Up: Nozioni base di relatività
Previous: Cenni di analisi tensoriale
Contents
Index
Simone Piccardi
2003-02-20
![]() un vettore a divergenza nulla; cioè:
un vettore a divergenza nulla; cioè:

![]() quello compreso fra due
ipersuperfici a
quello compreso fra due
ipersuperfici a ![]() costante e pari a
costante e pari a ![]() e
e ![]() (vedi 1.1), per tali superfici, con la convenzione di normale
esterna si ha:
(vedi 1.1), per tali superfici, con la convenzione di normale
esterna si ha:
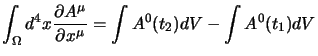
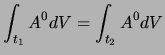

![]() e definiamo
e definiamo
![]() ,
dalla (1.33) si ottiene subito che:
,
dalla (1.33) si ottiene subito che: