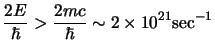Next: L'interazione col campo elettromagnetico
Up: Le soluzioni di particella
Previous: La costruzione di una
Contents
Index
Inconsistenze dell'equazione di Dirac
Visto tutto questo possiamo mostrare esplicitamente le inconsistenze che
emergono nell'uso dell'equazione di Dirac qualora si imponga, come si riteneva
di poter fare in un primo tempo, di utilizzare solo gli spinori ad energia
positiva, e pacchetti d'onde composti solo da quest'ultimi. Se questo è il caso
la corrente totale associata con una qualunque soluzione ad energia positiva
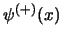 è data da:
è data da:
questa riscritta in termini degli spinori è:
qui al solito si integra su 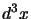 per avere la delta e su
per avere la delta e su  per mandarla
via e resta:
adesso per l'ultimo fattore possiamo sfruttare quanto ricavato dall'identità di
Gordon ottenendo che:
adesso teniamo conto che, considerando
per mandarla
via e resta:
adesso per l'ultimo fattore possiamo sfruttare quanto ricavato dall'identità di
Gordon ottenendo che:
adesso teniamo conto che, considerando
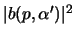 come la densità di
probabilità della soluzione di onda piana, la media è:
dove con questa notazione si è voluta intendere la media sul quadrimpulso
come la densità di
probabilità della soluzione di onda piana, la media è:
dove con questa notazione si è voluta intendere la media sul quadrimpulso 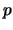 e
sulle soluzioni ad energia positiva; così nel nostro caso quello che si ottiene
è che:
e quindi la corrente totale per la sovrapposizione di soluzioni ad energia
positiva è proprio la velocità di gruppo. Questo è perfettamente coerente con
la teoria di Schroedinger, quello che non torna è l'assunzione di poter
descrivere pacchetti d'onda con la sovrapposizione di sole soluzioni ad
energia positiva. Per vederlo meglio consideriamo l'evoluzione temporale di
un pacchetto dato al tempo
e
sulle soluzioni ad energia positiva; così nel nostro caso quello che si ottiene
è che:
e quindi la corrente totale per la sovrapposizione di soluzioni ad energia
positiva è proprio la velocità di gruppo. Questo è perfettamente coerente con
la teoria di Schroedinger, quello che non torna è l'assunzione di poter
descrivere pacchetti d'onda con la sovrapposizione di sole soluzioni ad
energia positiva. Per vederlo meglio consideriamo l'evoluzione temporale di
un pacchetto dato al tempo 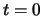 da una distribuzione di Gauss di larghezza a
mezza altezza
da una distribuzione di Gauss di larghezza a
mezza altezza  (che grosso modo rappresenta una particella localizzata
entro un volume sferico di raggio
(che grosso modo rappresenta una particella localizzata
entro un volume sferico di raggio  ); sia cioè:
questa, espressa in termini della
(2.111) per
); sia cioè:
questa, espressa in termini della
(2.111) per 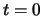 , ci dà:
adesso per determinare i coefficienti moltiplichiamo per
, ci dà:
adesso per determinare i coefficienti moltiplichiamo per
 ed integriamo su
ed integriamo su 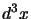 si ha:
adesso però un noto teorema delle trasformate di Fourier ci dice che:
per il secondo membro poi possiamo ottenere le solite delta di Dirac, ed
eliminarle attraverso l'integrazione su
si ha:
adesso però un noto teorema delle trasformate di Fourier ci dice che:
per il secondo membro poi possiamo ottenere le solite delta di Dirac, ed
eliminarle attraverso l'integrazione su  ; alla fine quello che resta
della precedente è:
adesso queste si trattano usando la
(2.105) e la analoga per
; alla fine quello che resta
della precedente è:
adesso queste si trattano usando la
(2.105) e la analoga per 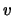 si ottiene:
e da queste si vede subito che se si vuole parlare di particella localizzata
sono necessarie anche le soluzioni ad energia negativa; se consideriamo poi il
rapporto
si ottiene:
e da queste si vede subito che se si vuole parlare di particella localizzata
sono necessarie anche le soluzioni ad energia negativa; se consideriamo poi il
rapporto 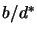 si ottiene subito che (i conti sono banali):
da cui si vede che
si ottiene subito che (i conti sono banali):
da cui si vede che 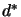 diventa rilevante quando
diventa rilevante quando  cresce fino a
diventare dell'ordine di
cresce fino a
diventare dell'ordine di  ; questo ci dice che se il pacchetto d'onde è
sparpagliato su una distanza
; questo ci dice che se il pacchetto d'onde è
sparpagliato su una distanza
 (la lunghezza d'onda Compton della
particella) l'esponenziale fa si che i termini con
(la lunghezza d'onda Compton della
particella) l'esponenziale fa si che i termini con
 siano
fortemente depressi e le soluzioni ad energia negativa siano trascurabili; ma
se si vuole localizzare la particella su una regione della stessa dimensione
della sua lunghezza d'onda Compton, cioè con
siano
fortemente depressi e le soluzioni ad energia negativa siano trascurabili; ma
se si vuole localizzare la particella su una regione della stessa dimensione
della sua lunghezza d'onda Compton, cioè con
 allora
l'esponenziale non serve più a deprimere le soluzioni ad energia negativa, che
invece diventano importanti; a questo punto allora la teoria di particella
singola viene meno e ci ritrova con le solite grane.
allora
l'esponenziale non serve più a deprimere le soluzioni ad energia negativa, che
invece diventano importanti; a questo punto allora la teoria di particella
singola viene meno e ci ritrova con le solite grane.
Un altro paradosso legato alle soluzioni ad energia negativa si ritrova nel
calcolo della corrente totale; non potendo fare a meno di escluderle
dall'espressione di un pacchetto d'onde dovremo scriverla in generale come:
qui si opera come nel caso precedente; si integra su 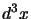 per ottenere
per ottenere
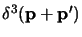 nei termini misti e le
nei termini misti e le
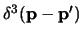 per gli altri; queste si eliminano reintegrando su
per gli altri; queste si eliminano reintegrando su 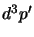 ; in ogni
caso si otterrà
; in ogni
caso si otterrà  , mentre per i termini misti sarà
, mentre per i termini misti sarà
 e negli
altri
e negli
altri  : per questi ultimi poi potremo procedere come nel caso precedente
usando le opportune identità di Gordon per cui alla fine si ottiene:
e adesso questa dipende dal tempo con un termine oscillante
dato dagli esponenziali ad una frequenza elevatissima che è:
: per questi ultimi poi potremo procedere come nel caso precedente
usando le opportune identità di Gordon per cui alla fine si ottiene:
e adesso questa dipende dal tempo con un termine oscillante
dato dagli esponenziali ad una frequenza elevatissima che è:





Next: L'interazione col campo elettromagnetico
Up: Le soluzioni di particella
Previous: La costruzione di una
Contents
Index
Simone Piccardi
2003-02-20
![]() è data da:
è data da:
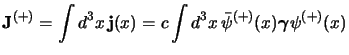
![$\displaystyle {\bf J}^{(+)}
= \int d^3x \int {d^3p d^3p'\over(2\pi\hbar)^6} {m^...
...'-p) x}\,\,
\bar u^{(\alpha)}(p) \boldsymbol{\gamma} u^{(\alpha')}(p')
\right]
$](img1234.png)
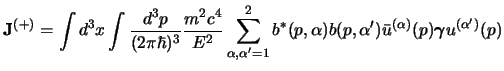
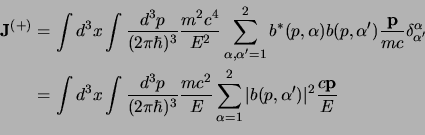
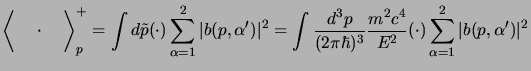
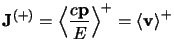

![\begin{displaymath}
\begin{aligned}
\left(
{1\over \pi d^2}
\right)^{3/4} &e^{-...
...bf p}\cdot {\bf x}} v^{(\alpha)}(p)
\right] \cr
\end{aligned}\end{displaymath}](img1245.png)
![\begin{displaymath}
\begin{aligned}
\int {d^3 x} & \, e^{-\ih {\bf p}\cdot {\bf ...
...p+p'})\cdot {\bf x}} v^{(\alpha)}(p)
\right]\cr
\end{aligned}\end{displaymath}](img1247.png)
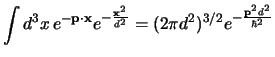
![$\displaystyle (4\pi d^2)^{3/4} e^{-\half{{\bf p}^2d^2\over \hbar^2}} u^{(1)}(mc...
...p,\alpha) u^{(\alpha)}(p) + d^*(\tilde p,\beta) v^{(\alpha)}(\tilde p)
\right]
$](img1249.png)
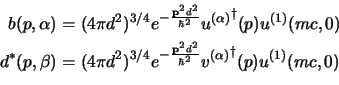
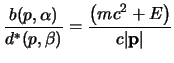
![\begin{displaymath}
\begin{aligned}
{\bf J}(t)
= c \int d^3x \int {d^3p d^3p'\...
...{(\alpha')}(p') e^{\ih p' x}
\right)
\bigg] \cr
\end{aligned}\end{displaymath}](img1258.png)
![\begin{displaymath}
\begin{aligned}
&{\bf J}(t)=c\int {d^3p\over(2\pi\hbar)^3} ...
...{\gamma} u^{(\alpha')}(\tilde p)
\right] \bigg\}
\end{aligned}\end{displaymath}](img1264.png)